Motivation

Let's revisit Runge's example from Chapter 2, Interpolation and Approximation, where we computed a Lagrange interpolation of Runge's function using eleven equally spaced nodes in the interval from -5 to 5:

In [1]: import numpy as np, matplotlib.pyplot as plt; \
   ...: from scipy.interpolate import BarycentricInterpolator
In [2]: def f(t): return 1. / (1. + t**2)
In [3]: nodes = np.linspace(-5, 5, 11); \
   ...: domain = np.linspace(-5, 5, 128); \
   ...: interpolant = BarycentricInterpolator(nodes, f(nodes))
In [4]: plt.figure(); \
   ...: plt.subplot(121); \
   ...: plt.plot(domain, f(domain), 'r-', label='original'); \
   ...: plt.plot(nodes, f(nodes), 'ro', label='nodes'); \
   ...: plt.plot(domain, interpolant1(domain), 'b--',
   ...:          label='interpolant'); \
   ...: plt.legend(loc=9); \
   ...: plt.subplot(122); \
   ...: plt.plot(domain, np.abs(f(domain)-interpolant1(domain))); \
   ...: plt.title('error or interpolation'); \
   ...: plt.show()

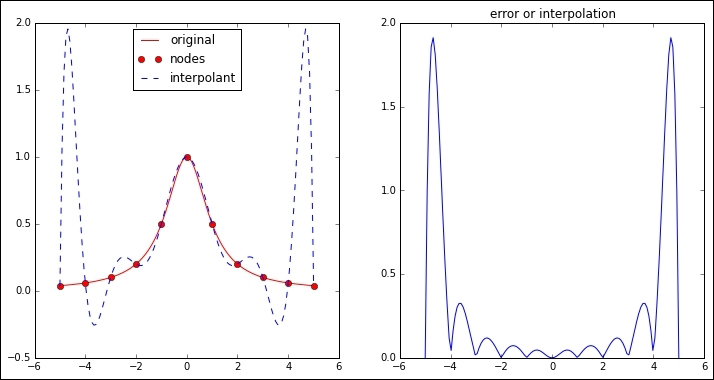
One way to measure...