Linear classification
Let's consider a generic linear classification problem with two classes. In the following figure, there's an example:
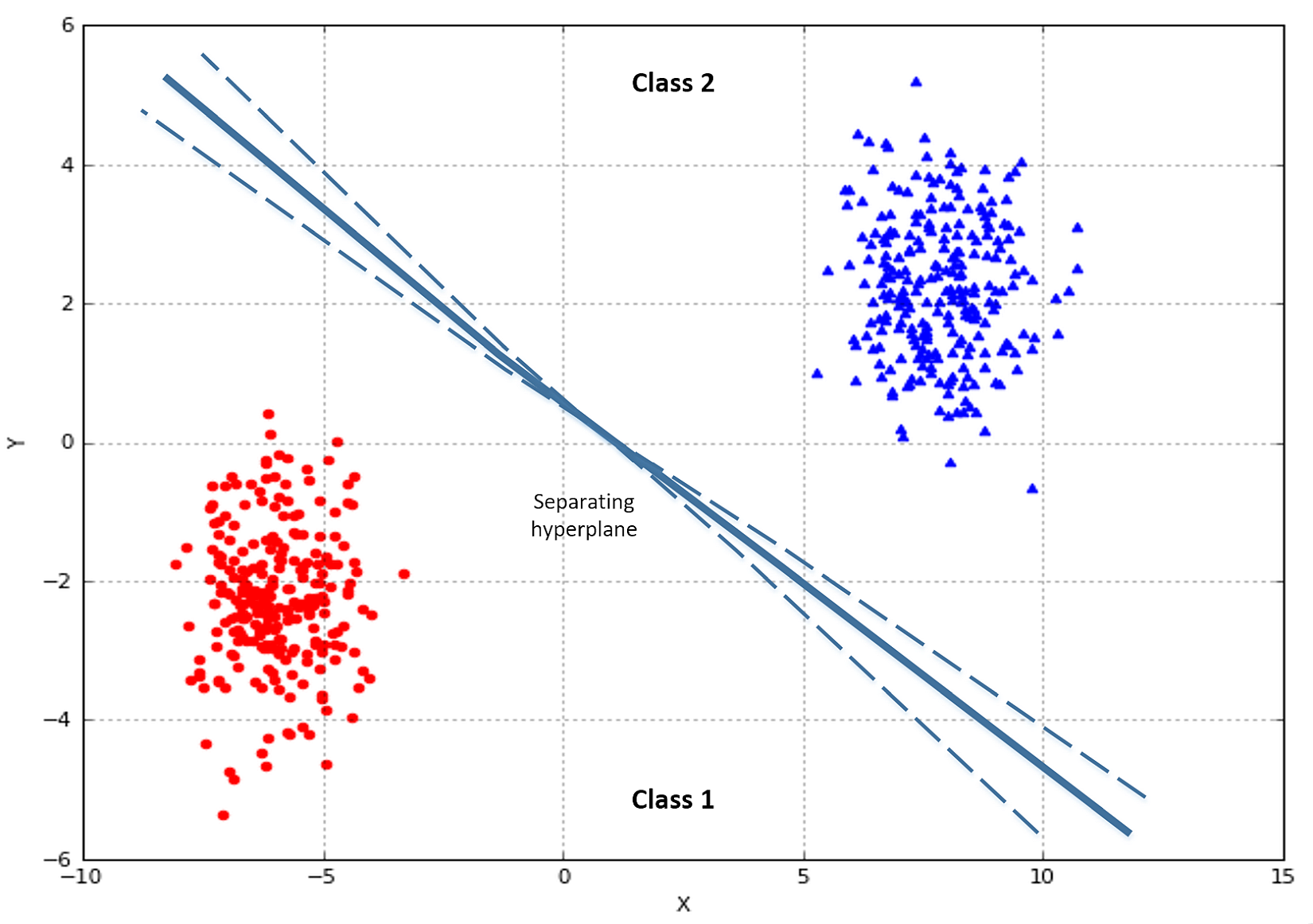
Our goal is to find an optimal hyperplane, which separates the two classes. In multi-class problems, the strategy one-vs-all is normally adopted, so the discussion can be focused only on binary classifications. Suppose we have the following dataset:
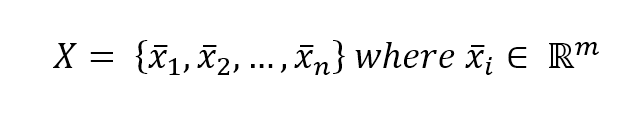
This dataset is associated with the following target set:
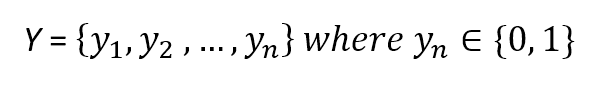
We can now define a weight vector made of m continuous components:
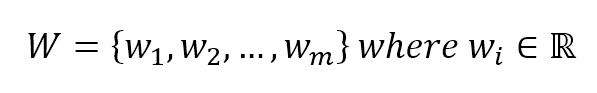
We can also define the quantity z:
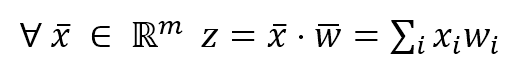
If x is a variable, z is the value determined by the hyperplane equation. Therefore, if the set of coefficients w that has been determined is correct, it happens that:
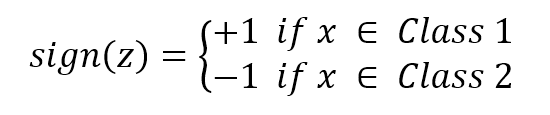
Now we must find a way to optimize w, in order to reduce the classification error. If such a combination exists (with a certain error threshold), we say that our problem is linearly separable. On the other hand, when it's impossible to find a linear classifier, the problem is called non-linearly...












































































