6.8 Markov and Chebyshev go to the casino
In this section, we work through the probability math of estimating π as we previously explored in section 1.5. We dropped coins into a square and looked at how many of them had their centers on or inside a circle. Chebyshev’s Inequality Markov, Andrey Chebyshev, Pafnuty
There are two important inequalities involving expected values, variances, and error terms. Let X be a finite random variable with a known distribution so that
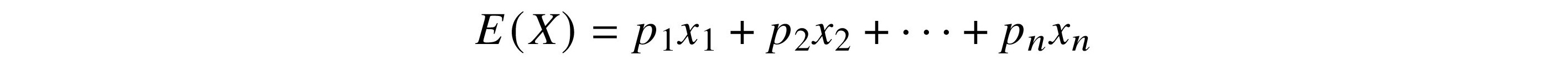
and each xk ≥ 0.
Markov’s Inequality
For a real number a > 0, Markov’s Inequality
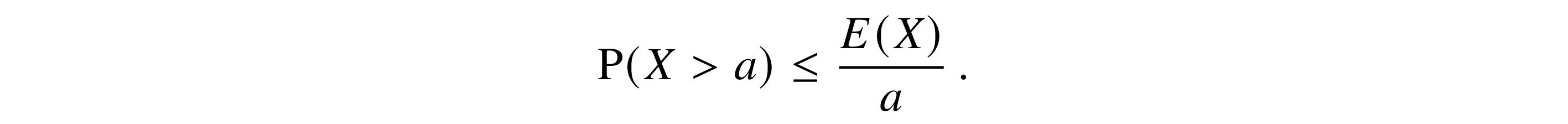
In Markov’s Inequality, the expression P(X > a) means “look at all the xk in X, and for all those where xk > a, add up the pk to get P(X > a).”
Exercise 6.8
Show that Markov’s Inequality holds for the distribution at the beginning of section 6.6 for...























































