Dijkstra algorithm
Edsger W. Dijkstra conceived his algorithm to solve the shortest path for graphs between 1956-1959.
His algorithm finds the shortest path between two nodes, but other variants exist to find the shortest paths between an origin and all other nodes; this is called a shortest path tree. Let's see how it works, and then we will implement it in Swift. We are going to explain it with the following example graph. We want the shortest path between node A and node E:

Shortest path example
The steps are as follows:
- The algorithm starts by marking the first node as the current node. It puts all the nodes as unvisited inside a set. It also initializes every node with a temporary distance, infinitum or a maximum number:
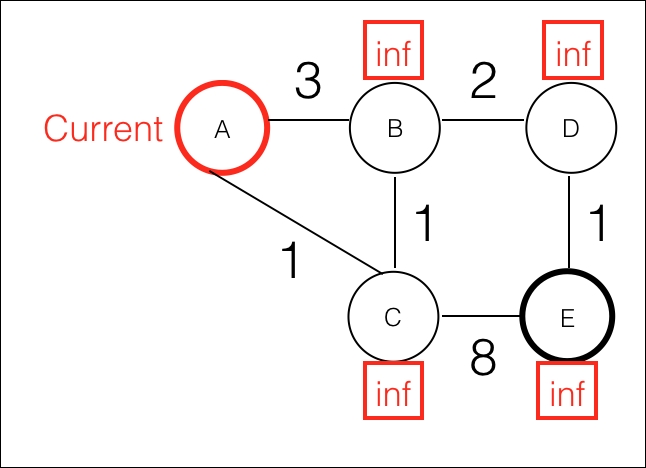
Shortest path step 1
- Then, for each unvisited neighbor of the current node, calculate the temporary distance from our current node to all its neighbors as the sum of the current node distance and edge weight to the neighbor for each case. If the result is smaller...































































