Basic data structures
Scalar
A scalar is a single number unlike a matrix or a vector. For example, 1.3 is a scalar. A scalar can be mathematically denoted as follows: 
Here, R is the real number space.
Vectors
A vector is an array of numbers. Unlike a set, where there is no order to elements, a vector has a certain order to the elements. An example vector is [1.0, 2.0, 1.4, 2.3]. Mathematically, it can be denoted as follows:
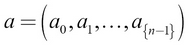
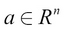
Alternatively, we can write this as:
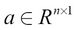
Here, R is the real number space and n is the number of elements in the vector.
Matrices
A matrix can be thought of as a two-dimensional arrangement of a collection of scalars. In other words, a matrix can be thought of as a vector of vectors. An example matrix would be as shown here:
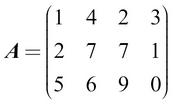
A more general matrix of size  can be mathematically defined like this:
can be mathematically defined like this:
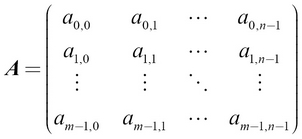
And:
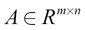
Here, m is the number of rows of the matrix, n is the number of columns in the matrix, and R is the real number space.
Indexing of a matrix
We will be using zero-indexed notation...



































































