Applying numeric methods
In the previous sections, you learned about a number of functions that range from inspecting data structures to math and logical operations. These functions are fundamental to solving problems such as root finding and doing calculus. As a computing environment, R already implements various tools of good performance so that users do not have to reinvent the wheel. In the following sections, you will learn the built-in functions designed for root finding and calculus.
Root finding
Root finding is a commonly encountered task. Suppose we want to find the roots of the following equation:
x2 + x - 2= 0
To manually find the roots, we can transform the preceding equation in product terms:
(x+2)(x-1)= 0
Therefore, the roots of the equation are x1= -2 and x2= 1.
In R, polyroot() can find roots of a polynomial equation in the form of:
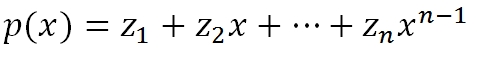
For the preceding problem, we need to specify the polynomial coefficient vector from zero order to the term of the highest order present in the equation...
























































