5.5 Matrix algebra
So far, we have looked at matrices and their relationships to linear maps. We now investigate operations on one or more matrices. We’ll first cover the general case of matrices which may have different numbers of rows and columns, and then move on to square matrices.
All matrices are over fields in this section, and when we manipulate multiple matrices, they all have entries in the same field. We can consider matrices over rings such as the integers, but we do not need to make this restriction for quantum computing.
5.5.1 Arithmetic of general matrices
Matrices of the same size, meaning they have the same number of rows and columns, can be added together entry by entry. For example,

The same is true for subtraction and negation:
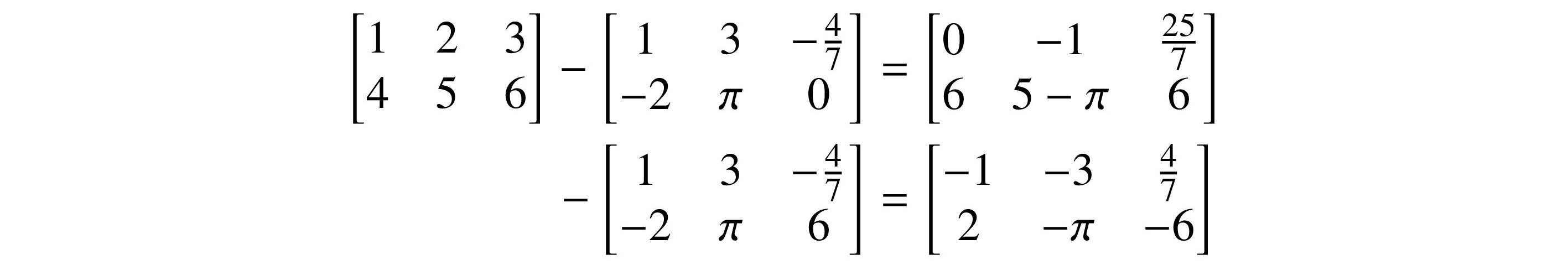
We multiply by a scalar entry by entry:

Exercise 5.12
Verify that the set of n-by-m matrices over a field...































































