5.4 Matrices
If we write out the details of a linear transformation of a five-dimensional vector space over a field F, it looks like this: matrix
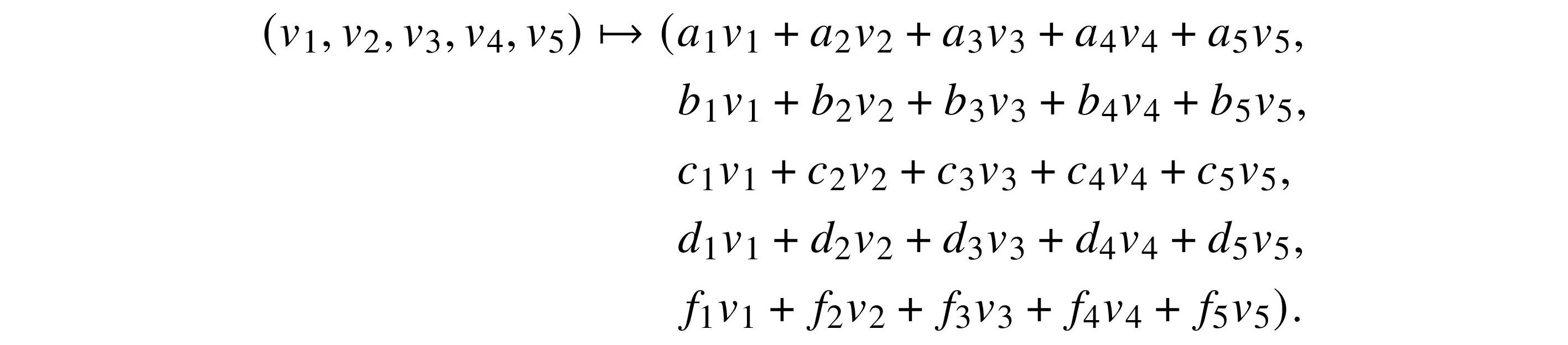
This notation is not practical, especially if we start looking at the formulas for compositions of linear maps. Hence, we introduce matrices.
We begin with notation and then move on to the algebra.
5.4.1 Notation and terminology
This array of values with entries in the field F

is a 3-by-4 matrix: it has three rows, four columns, and 12 = 3 × 4 entries. The dimension of this matrix is 3-by-4. matrix$dimension matrix$entry
When we need subscripts for the entries in a matrix, they look like this:

for a 3-by-3 matrix. The first subscript is the row index, and the second is the column index. matrix$row index matrix$column index
In mathematics and physics, we use 1 as the first row or column index. In computer science and...































































