Poisson Regression
In linear regression, we saw an equation of the form:
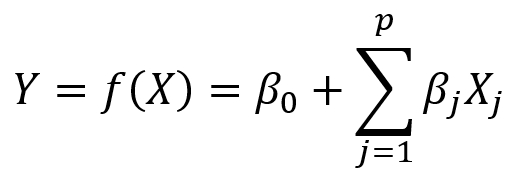
In Poisson Regression, the response variable Y is a count or rate (Y/t) that has a Poisson distribution with expected (mean) count of  as
as  , which is equal to variance.
, which is equal to variance.
In case of logistic regression, we would probe for values that can maximize log-likelihood to get the maximum likelihood estimators (MLEs) for coefficients.
There are no closed-form solutions, hence the estimations of maximum likelihood would be obtained using iterative algorithms such as Newton-Raphson and Iteratively re-weighted least squares (IRWLS).
Poisson regression is suitable for the count-dependent variable, which must meet the following guidelines:
It follows a Poisson distribution
Counts are not negative
Values are whole numbers (no fractions)
Note
The dataset used here to demonstrate Poisson regression comes from A. Colin Cameron and Per Johansson, "Count Data Regression Using Series Expansion: With Applications", Journal of Applied Econometrics, Vol...












































































