2. Mutual Information and Entropy
MI can also be interpreted in terms of entropy. Recall from Chapter 6, Disentangled Representation GANs, that entropy, H(X), is a measure of the expected amount of information of a random variable X:
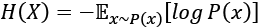 (Equation 13.2.1)
(Equation 13.2.1)Equation 13.2.1 implies that entropy is also a measure of uncertainty. The occurrence of uncertain events gives us a higher amount of surprise, or information. For example, news about an employee's unexpected promotion has a high amount of information, or entropy.
Using Equation 13.2.1, MI can be expressed as:
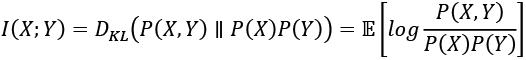
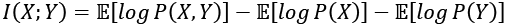
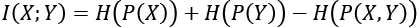
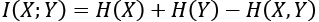 (Equation 13.2.2)
(Equation 13.2.2)Equation 13.2.2 implies that MI increases with marginal entropy but decreases with joint entropy. A more common expression for MI in terms of entropy is as follows:
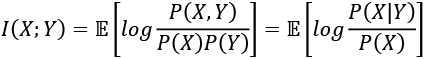
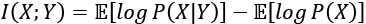
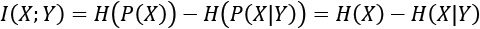 (Equation 13.2.3)
(Equation 13.2.3)Equation 13.2.3 tells us that MI increases with the entropy of a random variable but decreases with the conditional entropy on another random variable. Alternatively...











































































