Once the model is built, how do we know it will perform on new data? Is this model any good? To answer these questions, we'll first look into the model generalization, and then see how to get an estimate of the model performance on new data.
Generalization and evaluation
Underfitting and overfitting
Predictor training can lead to models that are too complex or too simple. The model with low complexity (the leftmost models in the following diagram) can be as simple as predicting the most frequent or mean class value, while the model with high complexity (the rightmost models) can represent the training instances. Modes that are too rigid, shown on the left-hand side, cannot capture complex patterns; while models that are too flexible, shown on the right-hand side, fit to the noise in the training data. The main challenge is to select the appropriate learning algorithm and its parameters, so that the learned model will perform well on the new data (for example, the middle column):
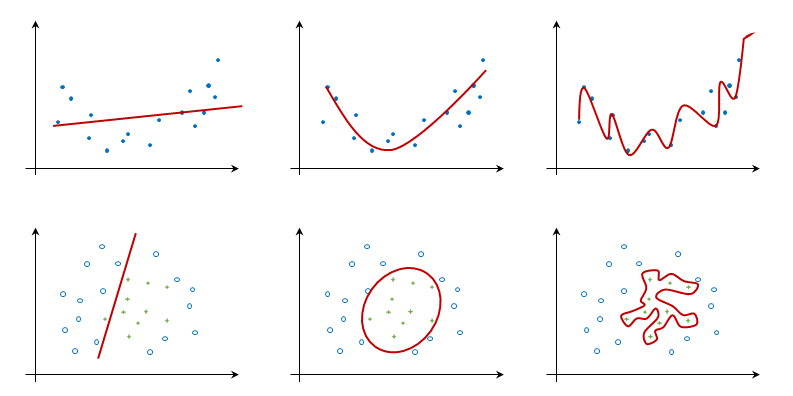
The following diagram shows how errors in the training set decreases with model complexity. Simple rigid models underfit the data and have large errors. As model complexity increases, it describes the underlying structure of the training data better and, consequentially, the error decreases. If the model is too complex, it overfits the training data and its prediction error increases again:
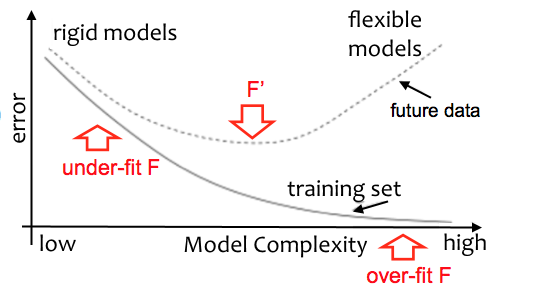
Depending on the task complexity and data availability, we want to tune our classifiers toward more or less complex structures. Most learning algorithms allow such tuning, as follows:
- Regression: This is the order of the polynomial
- Naive Bayes: This is the number of the attributes
- Decision trees: This is the number of nodes in the tree—pruning confidence
- K-nearest neighbors: This is the number of neighbors—distance-based neighbor weights
- SVM: This is the kernel type; cost parameter
- Neural network: This is the number of neurons and hidden layers
With tuning, we want to minimize the generalization error; that is, how well the classifier performs on future data. Unfortunately, we can never compute the true generalization error; however, we can estimate it. Nevertheless, if the model performs well on the training data but performance is much worse on the test data, then the model most likely overfits.
Train and test sets
To estimate the generalization error, we split our data into two parts: training data and testing data. A general rule of thumb is to split them by the training: testing ratio, that is, 70:30. We first train the predictor on the training data, then predict the values for the test data, and finally, compute the error, that is, the difference between the predicted and the true values. This gives us an estimate of the true generalization error.
The estimation is based on the two following assumptions: first, we assume that the test set is an unbiased sample from our dataset; and second, we assume that the actual new data will reassemble the distribution as our training and testing examples. The first assumption can be mitigated by cross-validation and stratification. Also, if it is scarce, one can't afford to leave out a considerable amount of data for a separate test set, as learning algorithms do not perform well if they don't receive enough data. In such cases, cross-validation is used instead.
Cross-validation
Cross-validation splits the dataset into k sets of approximately the same size—for example, in the following diagram, into five sets. First, we use sets 2 to 5 for learning and set 1 for training. We then repeat the procedure five times, leaving out one set at a time for testing, and average the error over the five repetitions:
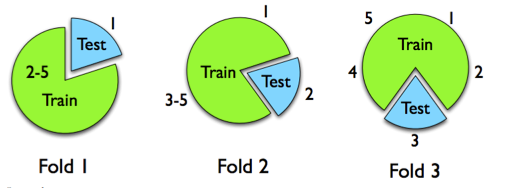
This way, we use all of the data for learning and testing as well, while avoiding using the same data to train and test a model.
Leave-one-out validation
An extreme example of cross-validation is the leave-one-out validation. In this case, the number of folds is equal to the number of instances; we learn on all but one instance, and then test the model on the omitted instance. We repeat this for all instances, so that each instance is used exactly once for the validation. This approach is recommended when we have a limited set of learning examples, for example, less than 50.
Stratification
Stratification is a procedure to select a subset of instances in such a way that each fold roughly contains the same proportion of class values. When a class is continuous, the folds are selected so that the mean response value is approximately equal in all of the folds. Stratification can be applied along with cross-validation or separate training and test sets.





































































