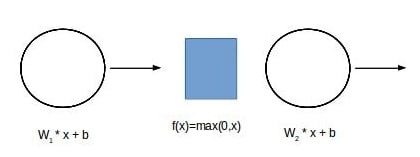The second function of the neuron is the activation function, which is tasked with introducing a nonlinearity between neurons. A commonly used activation is the sigmoid activation, which you may be familiar with from logistic regression. It squeezes the output of the neuron into an output space where very large values of z are driven to 1 and very small values of z are driven to 0.
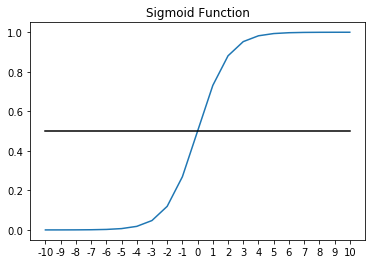
The sigmoid function looks like this:
It turns out that the activation function is very important for intermediate neurons. Without it one could prove that a stack of neurons with linear activation's (which is really no activation, or more formally an activation function where z=z) is really just a single linear function.
A single linear function is undesirable in this case because there are many scenarios where our network may be under specified for the problem at hand. That is to say that the network can't model the data well because of non-linear relationships present in the data between the input features and target variable (what we're predicting).
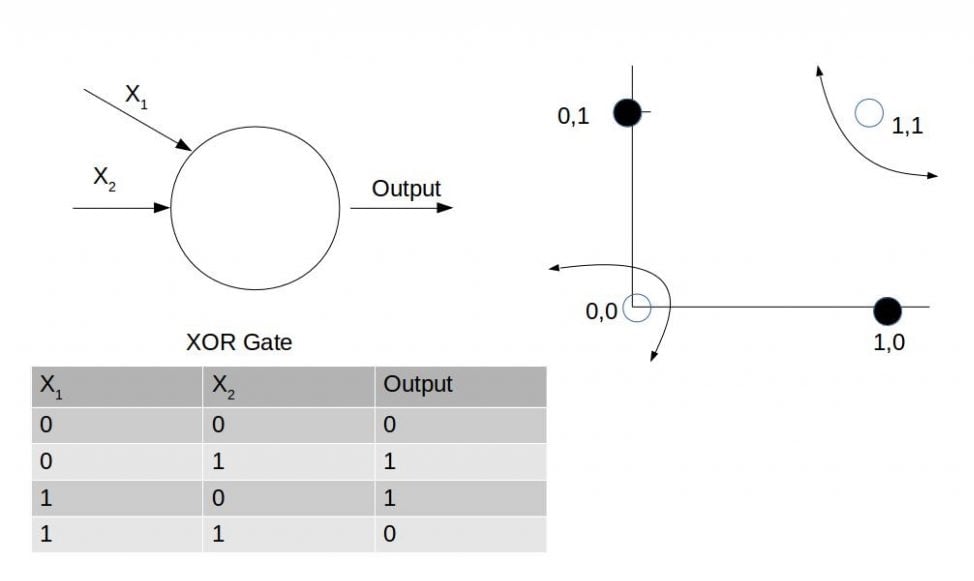
The canonical example of a function that cannot be modeled with a linear function is the exclusive OR function, which is shown in the following figure:
Other common activation functions are the tanh function and the ReLu or Rectilinear Activation.
The hyperbolic tangent or the tanh function looks like this:
>
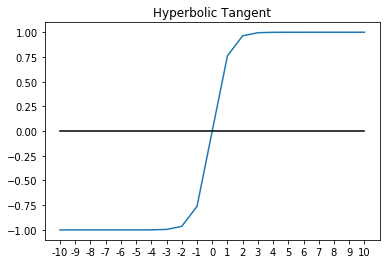
The tanh usually works better than sigmoid for intermediate layers. As you can probably see, the output of tanh will be between [-1, 1], whereas the output of sigmoid is [0, 1]. This additional width provides some resilience from a phenomenon known as the vanishing/exploding gradient problem, which we will cover in more detail later. For now, it's enough to know that the vanishing gradient problem can cause networks to converge very slowly in the early layers, if at all. Because of that, networks using tanh will tend to converge somewhat faster than networks that use sigmoid activation. That said, they are still not as fast as ReLu.
ReLu, or Rectilinear Activation, is defined simply as:
It's a safe bet and we will use it most of the time throughout this book. Not only is ReLu easy to compute and differentiate, it's also resilient against the vanishing gradient problem. The only drawback to ReLu is that it's first derivative is undefined at exactly 0. Variants including leaky ReLu, are computationally harder, but more robust against this issue.
For completeness, here's a somewhat obvious graph of ReLu: