5.13 Systems of linear equations
The two equations

together are an example of a system of linear equations. On the left of the equal signs are linear expressions, and on the right are constants. In R2, these represent two lines. In general, two lines in R2 may be the same, be parallel and so never intersect, or intersect at a single point.
If we use subscripted variables, the same relationship might be expressed by
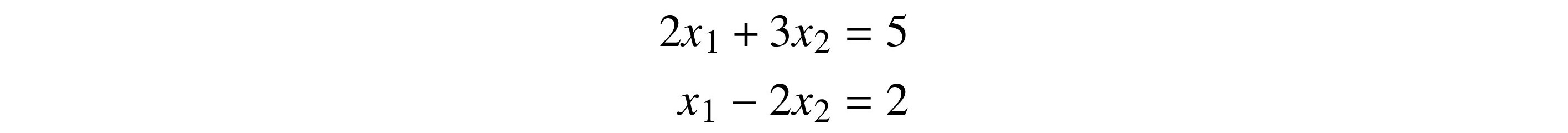
We can further rewrite this in matrix and vector form as

If we let

then our system is simply Ax = b. This is a standard form for writing such systems of any dimension, and we call it a linear equation. linear$equation
Our goal may be to solve for all of x, learn only some of the xj, or understand some function f applied to x. If A is invertible, then

In this case, there is one possible value for x. If A is not invertible, then there might be no solution or a vector space...
































































