Now, let's look at our first approach to dimensionality reduction, using PCA. In this section, we will learn all about PCA. We will see what PCA does, and also show approaches to evaluating the quality of principal components.
We'll start with a dataset. This dataset lies in some dimensional space. In each dimension, the data varies. There's no necessary relationship in this variation. Furthermore, there could be correlations between the coordinates. This is better represented using the following diagram:

With PCA, we find a new feature space based on linear combinations of the original feature space, with new features, called principal components, as shown in the following diagram:
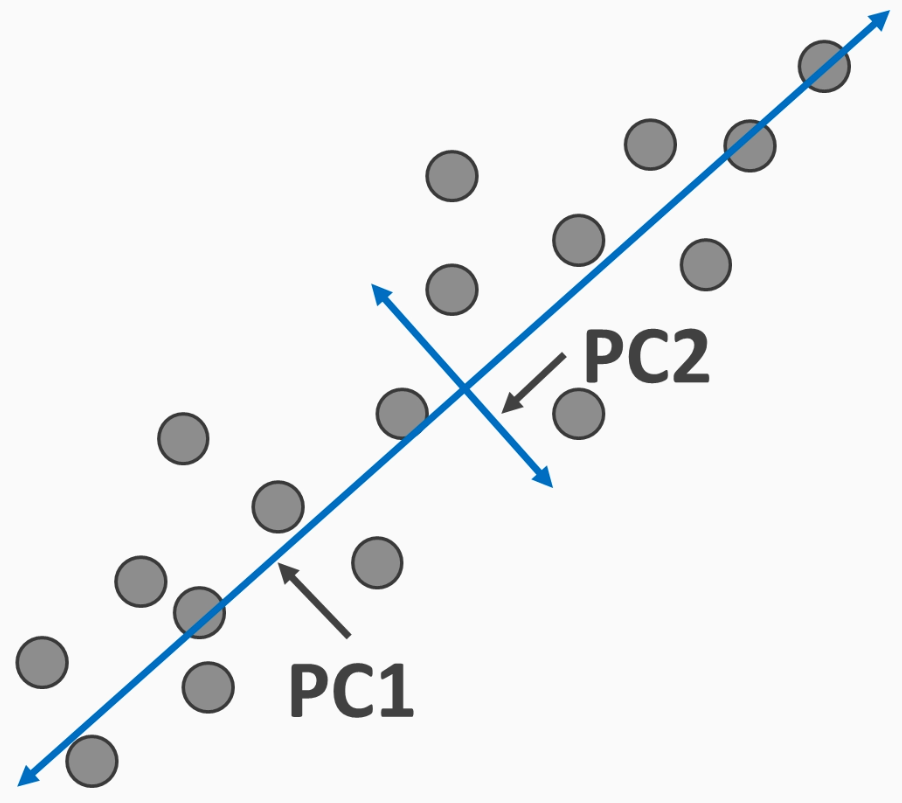
The principal components are all uncorrelated. Additionally, the variance of the dataset with respect to each principal component is decreasing. The first...

































































