Markov decision processes and Bellman equations
Markov decision process (MDP) formally describes an environment for reinforcement learning. Where:
- Environment is fully observable
- Current state completely characterizes the process (which means the future state is entirely dependent on the current state rather than historic states or values)
- Almost all RL problems can be formalized as MDPs (for example, optimal control primarily deals with continuous MDPs)
Central idea of MDP: MDP works on the simple Markovian property of a state; for example, St+1 is entirely dependent on latest state St rather than any historic dependencies. In the following equation, the current state captures all the relevant information from the history, which means the current state is a sufficient statistic of the future:
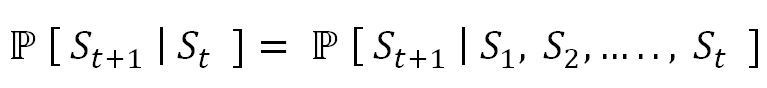
An intuitive sense of this property can be explained with the autonomous helicopter example: the next step is for the helicopter to move either to the right, left, to pitch, or to roll, and so on, entirely...

























































