In linear regression, only the residual sum of squares (RSS) is minimized, whereas in ridge and lasso regression, a penalty is applied (also known as shrinkage penalty) on coefficient values to regularize the coefficients with the tuning parameter λ.
When λ=0, the penalty has no impact, ridge/lasso produces the same result as linear regression, whereas λ -> ∞ will bring coefficients to zero:
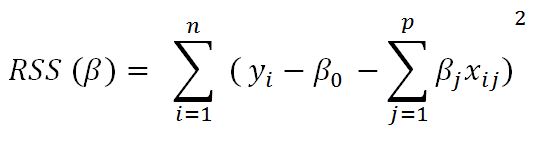
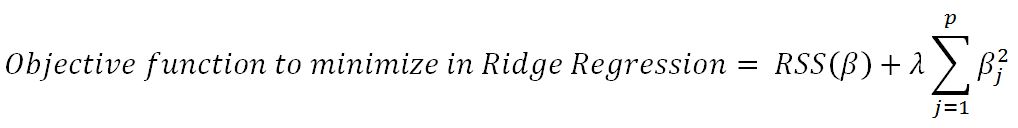
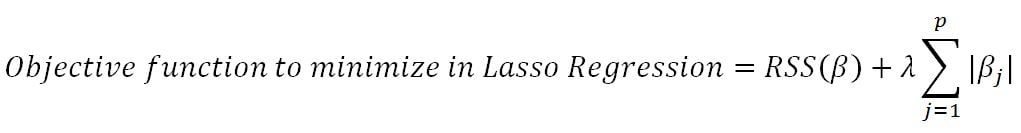
Before we go deeper into ridge and lasso, it is worth understanding some concepts on Lagrangian multipliers. One can show the preceding objective function in the following format, where the objective is just RSS subjected to cost constraint (s) of budget. For every value of λ, there is an s such that will provide the equivalent equations, as shown for the overall objective function with a...

























































