Tessellating a curve
In this recipe, we'll take a look at the basics of tessellation shaders by drawing a cubic Bezier curve. A Bezier curve is a parametric curve defined by four control points. The control points define the overall shape of the curve. The first and last of the four points define the start and end of the curve, and the middle points guide the shape of the curve, but do not necessarily lie directly on the curve itself. The curve is defined by interpolating the four control points using a set of blending functions. The blending functions define how much each control point contributes to the curve for a given position along the curve. For Bezier curves, the blending functions are known as the Bernstein polynomials.
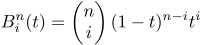
In the preceding equation, the first term is the binomial coefficient function (shown in the following equation), n is the degree of the polynomial, i is the polynomial number, and t is the parametric parameter.
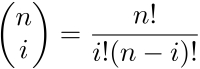
The general parametric form for the Bezier curve is then...


























































