The central limit theorem

A random sample is a set of numbers S = {x₁, x₂,... , x_n}, each of which is a measurement of some unknown value that we seek. We can assume that each x_i is a value of a random variable X_i, and that all these random variables X₁, X₂,…, X_n are independent and have the same distribution with mean μ and standard deviation σ. Let S_n and Z be the random variables:

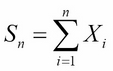
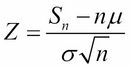
The central limit theorem states that the random variable Z tends to be normally distributed as n gets larger. That means that the PDF of Z will be close to the function φ(x) and the larger n is, the closer it will be.

By dividing numerator and denominator by n, we have this alternative formula for Z:

This isn't any simpler. But if we designate the random variable as:

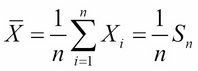
then we can write Z as:

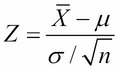
The central limit theorem tells us that this standardization of the random variable is nearly distributed as the standard normal distribution φ(x). So, if we take n measurements x₁, x₂,…, x_n of an unknown quantity that has...