Now that you understand the basic concepts of searching, we'll look at how DFS works by using the three basic ingredients of search algorithms—the initial state, the successor function, and the goal function. We will use the stack data structure.
Let's first represent the DFS algorithm in the form of a flowchart, to offer a better understanding:
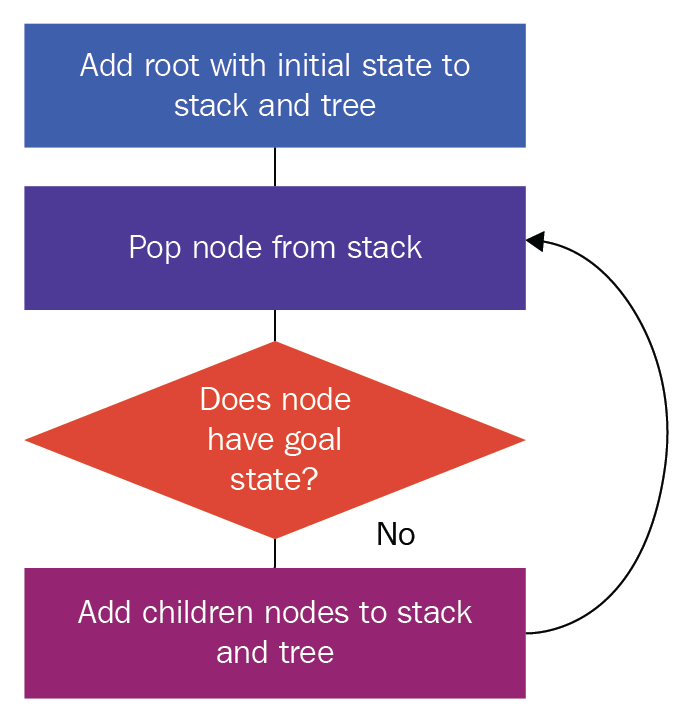
The steps in the preceding flowchart are as follows:
- We create a root node using the initial state, and we add this to our stack and tree
- We pop a node from the stack
- We check whether it has the goal state; if it has the goal state, we stop our search here
- If the answer to the condition in step 3 is No, then we find the child nodes of the pop node, and add them to the tree and stack
- We repeat steps 2 to 4 until we either find the goal state or exhaust all of the nodes in the search tree
Let's apply the preceding algorithm to our filesystem, as follows:
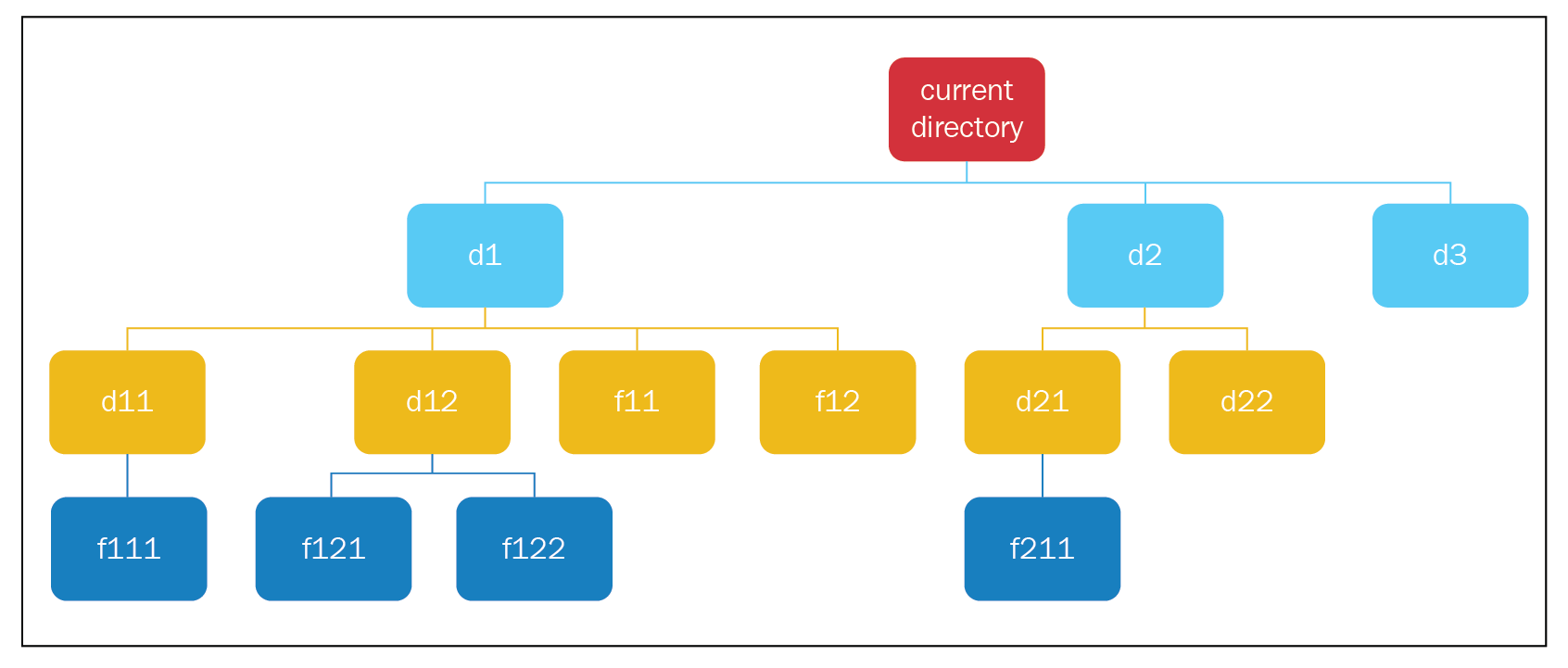
- We create our root node, add it to the search tree, and add it to the stack. We pop a node from the stack, which is the current directory node.
- The current directory node doesn't have the goal state, so we find its child nodes and add them to the tree and stack.
- We pop a node from the stack (d1); it doesn't have the goal state, so we find its child nodes and add it to the tree and stack.
- We pop a node from the stack (d11); it doesn't have the goal state, so we find its child node, add it to the tree and stack.
- We pop a node (f111); it doesn't have the goal state, and it also doesn't have child nodes, so we carry on.
- We pop the next node, d12; we find its child nodes and add them to the tree and stack.
- We pop the next node, f121, and it doesn't have any child nodes, so we carry on.
- We pop the next node, f122, and it doesn't have any child nodes, so we carry on.
- We pop the next node, f11, and we encounter the same case (where we have no child nodes), so we carry on; the same goes for f12.
- We pop the next node, d2, and we find its child nodes and add them to the tree and stack.
- We pop the next node, d21, and we find its child node and add it to the tree and stack.
- We pop the next node, f211, and we find that it has the goal state, so we end our search here.
Let's try to implement these steps in code, as follows:
...
from Node import Node
from State import State
def performStackDFS():
"""
This function performs DFS search using a stack
"""
#create stack
stack = []
#create root node and add to stack
initialState = State()
root = Node(initialState)
stack.append(root)
...
We have created a Python module called StackDFS.py, and it has a method called performStackDFS(). In this method, we have created an empty stack, which will hold all of our nodes, the initialState, a root node containing the initialState, and finally we have added this root node to the stack.
Remember that in Stack.py, we wrote a while loop to process all of the items in the stack. So, in the same way, in this case we will write a while loop to process all of the nodes in the stack:
...
while len(stack) > 0:
#pop top node
currentNode = stack.pop()
print "-- pop --", currentNode.state.path
#check if this is goal state
if currentNode.state.checkGoalState():
print "reached goal state"
break
#get the child nodes
childStates = currentNode.state.successorFunction()
for childState in childStates:
childNode = Node(State(childState))
currentNode.addChild(childNode)
...
As shown in the preceding code, we pop the node from the top of the stack and call it currentNode(), and then we print it so that we can see the order in which the nodes are processed. We check whether the current node has the goal state, and if it does, we end our execution here. If it doesn't have the goal state, we find its child nodes and add it under currentNode, just like we did in NodeTest.py.
We will also add these child nodes to the stack, but in reverse order, using the following for loop:
...
for index in range(len(currentNode.children) - 1, -1, -1):
stack.append(currentNode.children[index])
#print tree
print "----------------------"
root.printTree()
...
Finally, when we exit the while loop, we print the tree. Upon successful execution of the code, we will get the following output:
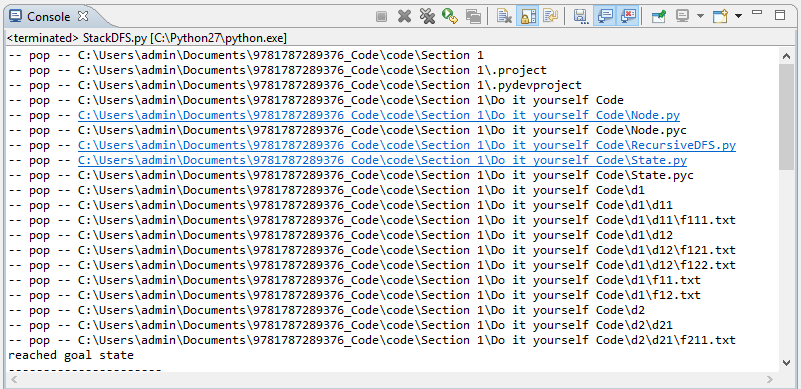
The output displays the order in which the nodes are processed, and we can see the first node of the tree. Finally, we encounter our goal state, and our search stops:
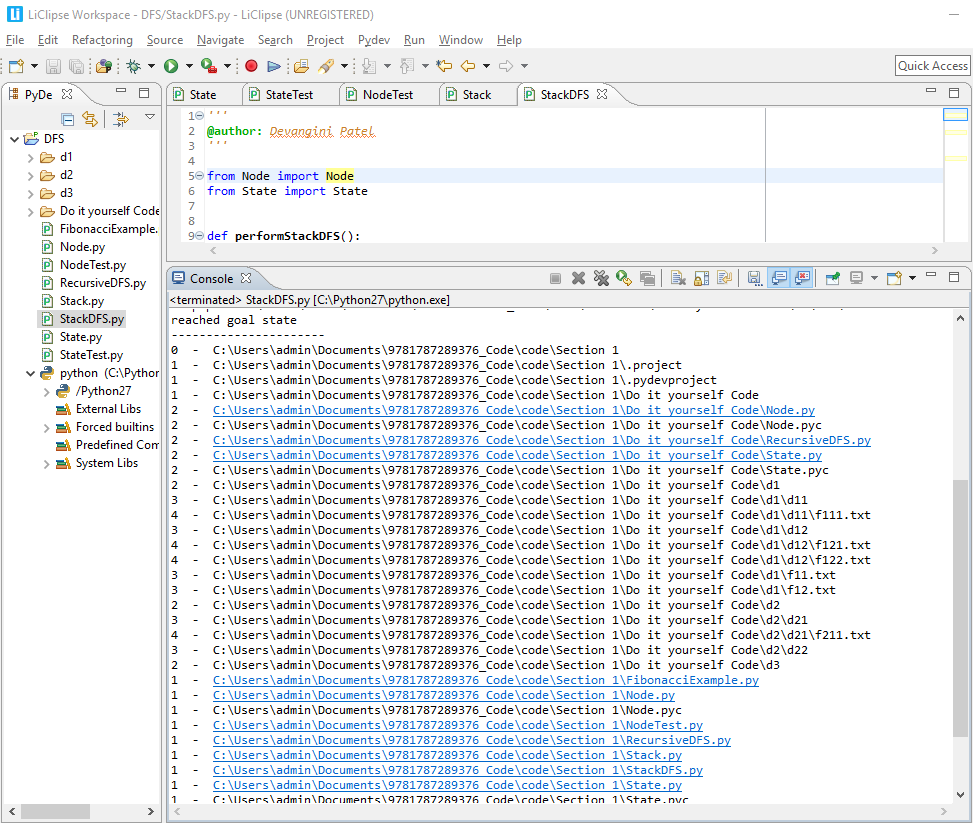
The preceding screenshot displays the search tree. Note that the preceding output and the one before it are almost the same. The only difference is that in the preceding screenshot, we can find two nodes, d22 and d3, because their parent nodes were explored.


































































