Performance Measurement
The most important aspect of optimization is the measurement of code execution time. Unless we measure our application's performance with a wide range of input datasets, we will have no clue as to which part takes the most time and, our optimization efforts will be shot in the dark, with no guarantee of a result. There are several approaches for measurement, and some of them are listed here:
- Runtime instrumentation or profiling
- Source code instrumentation
- Manual execution timing
- Studying generated assembly code
- Manual estimation by studying the code and algorithms used
The preceding list is ordered in terms of how accurate the measurement is (with the most accurate one first). However, each of these methods has different advantages. The choice of which approach to adopt depends on the goals and scope of the optimization effort. In an all-out effort to get the fastest possible implementation, all of these may be required. We will examine each of these approaches in the following sections.
Manual Estimation
The biggest possible improvement in performance occurs when we replace an algorithm with a superior one. For example, consider the two versions of a trivial function that sums the integers from 1 to n:
int sum1(int n)
{
int ret = 0;
for(int i = 1; i <= n; ++i)
{
ret += i;
}
return ret;
}
int sum2(int n)
{
return (n * (n + 1)) / 2;
}
The first function, sum1, uses a simple loop to calculate the sum and has a runtime complexity that is proportional to n, whereas the second function, sum2, uses the algebraic summation formula and takes constant time independent of n. In this quite contrived example, we have optimized a function simply by using the basic knowledge of algebra.
There are many well-known algorithms for every conceivable operation that have been proven to be the most optimal. The best way to make our code run as fast as possible is by using algorithms.
It is essential to have a vocabulary of algorithms. We do not need to be an algorithm expert, but we need to at least be aware of the existence of efficient algorithms in various domains, even if we are not capable of implementing them from scratch. A slightly deeper knowledge of algorithms will help us find parts of our program that perform similar, if not exactly the same, computations as well-known algorithms. Certain code features such as nested loops or linear scanning of data are often obvious candidates for improvement, provided we can verify that these constructs are within hotspots in the code. A hotspot is a section of code that runs very often and affects performance significantly. The C++ standard library includes a lot of basic algorithms that can be used as building blocks to improve the efficiency of many common operations.
Studying Generated Assembly Code
Assembly language is a human readable representiation of the binary machine code that actually executes on the processor. For any serious programmer of a compiled language such as C++, a basic understanding of assembly language is a great asset.
Studying the generated assembly code for a program can give us some good insights into how the compiler works and estimates of code efficiency. There are many cases where this is the only approach possible to determine efficiency bottlenecks.
Apart from this, a basic knowledge of assembly language is essential to be able to debug C++ code since some of the most difficult bugs to catch are those related to the low-level generated code.
A very powerful and popular online tool that's used for analyzing compiler-generated code is the Compiler Explorer that we will be using in this chapter.
Note
The Godbolt compiler explorer can be found at https://godbolt.org.
The following is a screenshot of the Godbolt compiler explorer:
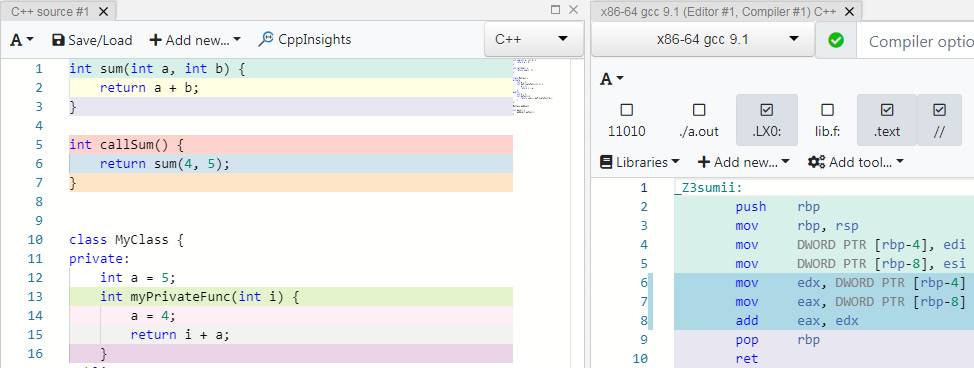
Figure 8.1: Godbolt compiler explorer
As you can see, the Godbolt compiler explorer consists of two panes. The one on the left is where we type the code in, while the one on the right displays the generated assembly code. The left-hand pane has a dropdown so that we can choose the desired language. For our purposes, we will use the C++ language with the gcc compiler.
The right-hand pane has options that we can use to choose a compiler version. Almost all the versions of popular compilers such as gcc, clang, and cl (Microsoft C++) are present, including the ones for non-X86 architectures such as ARM.
Note
We will refer to the Intel processor architecture as x86 for simplicity, even though the correct definition is x86/64. We will skip mentioning the "64" since almost all processors being manufactured today are 64-bit. Even though x86 was invented by Intel, now all PC processor manufacturers are licensed to use it.
In order to get familiar with the basics of the Compiler Explorer tool and understand the x86 assembly code at a basic level, let's examine the assembly code generated by a compiler for a simple function that sums up the integers from 1 to N. Here is the sum function that needs to be written in the left-hand pane of the Compiler Explorer:
int sum(int n)
{
int ret = 0;
for(int i = 1; i <= n; ++i)
{
ret += i;
}
return ret;
}
In the right-hand pane, the compiler must be set to x86-64 gcc 8.3, like this:
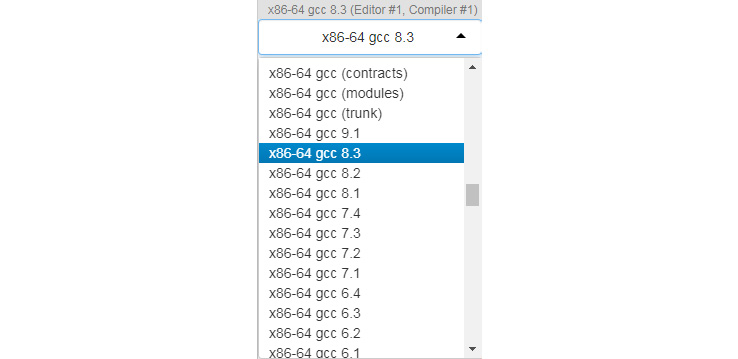
Figure 8.2: C++ compiler
Once this is done, the left-hand pane's code is automatically recompiled and the assembly code is generated and displayed on the right-hand pane. Here, the output is color-coded to show which lines of assembly code is generated from which lines of C++ code. The following screenshot shows the assembly code that was generated:
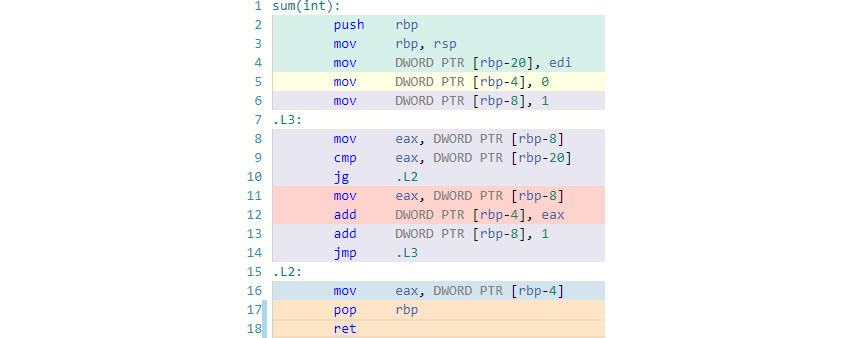
Figure 8.3: Assembly result
Let's analyze the preceding assembly code briefly. Each instruction in the assembly language consists of an opcode and one or more operands, which can be registers, constant values, or memory addresses. A register is a very fast storage location in the CPU. In the x86 architecture, there are eight main registers, namely RAX, RBX, RCX, RDX, RSI, RDI, RSP, and RBP. The Intel x86/x64 architecture uses a curious pattern of register naming:
- RAX is a general-purpose 64-bit integer register.
- EAX refers to the bottom 32 bits of RAX.
- AX refers to the bottom 16 bits of EAX.
- AL and AH refer to the bottom and top 8 bits of AX, respectively.
The same convention applies to other general-purpose registers such as RBX, RCX, and RDX. The RSI, RDI, and RBP registers have 16-bit and 32-bit versions but not the 8-bit sub-registers. The opcode of an instruction can be of several types including arithmetic, logical, bitwise, comparison or jump operations. It is common to refer to an opcode as an instruction. For example, "mov instruction" means an instruction whose opcode is mov. Here is the snapshot of the assembly code for our sum function:

Figure 8.4: Assembly code of the sum function
In the preceding screenshot, the first few lines are called a function prologue, that is, the instructions that are used to set up the stack frame and local variables. A stack frame represents the localized data in a function that includes the arguments and the local variables. When the function returns, the stack frame is discarded. The mov instruction initializes a register or memory location with a constant value. The syntax of the assembly code here is called Intel syntax. The convention with this syntax is that the destination operand is always the first one. For example, the MOV RAX, RBX assembly code means move the value in the RBX register to the RAX register.
Note
Assembly language is usually not case-sensitive, so EAX and eax mean the same thing.
The DWORD PTR [rbp-8] expression in assembly is equivalent to the (*(DWORD*)(rbp - 8)) C expression. In other words, the memory address rbp-8 is accessed as a 4 byte DWORD (a double word of memory – 32 bits). The square brackets in assembly code represent dereferencing, much like the * operator in C/C++. The rbp register is the base pointer that always contains the address of the base of the currently executing functions stack. It is not essential to know how exactly this stack frame works but remember that since the stack starts at a higher address and moves down, function arguments and local variables have addresses as negative offsets from rbp. If you see some negative offset from rbp, it refers to a local variable or argument.
In the preceding screenshot, the first mov instruction puts the value from the edi register onto the stack—in this case, it represents the n argument that was passed in. The last two mov instructions initialize the ret variable and the i loop variable in our code to 0 and 1, respectively.
Now, examine the snapshot of the assembly code that follows the prologue and initialization – this is our for() loop:

Figure 8.5: Assembly code of the for loop
In the preceding screenshot, the lines that have a string followed by a colon are called labels. They're very similar to labels in programming languages such as BASIC, C/C++, or Pascal and are used as targets of jump instructions (the assembly language equivalent of goto statements).
Instructions starting with J on x86 assembly are all jump instructions, such as JMP, JG, JGE, JL, JLE, JE, JNE, and so on. Jump instructions are conditional or unconditional gotos. In the preceding screenshot, the mov instruction loads the value of the i variable from memory to the eax register. Then, it is compared against the n value in memory with the cmp instruction.
Note
The JG instruction here means jump if greater.
If the comparison was greater, then the execution jumps to the .L2 label (which is outside the loop). If not, the execution continues with the next instruction, like so:

Figure 8.6: Assembly code of the next instruction
Here, the value of i is reloaded again into eax, which seems unnecessary. But remember that this assembly code is not optimized, so the compiler has generated code that would be suboptimal and may include unnecessary work. Then, the value in eax is added to ret, after which 1 is added to i. Finally, the execution jumps back to the.L3 label. These instructions between the .L2 and .L3 labels form the code that executes the for loop and sums up the sequence of integers up to n, like so:

Figure 8.7: Assembly code of the for loop
This is called the function epilog. First, the value to be returned, ret, is moved into the eax register – this is typically the register where the return value of a function is stored. Then, the stack frame is reset and finally ret returns from the sum() function.
Note
The "ret" in the above assembly listing is the mnemonic for the RETURN instruction and should not be confused with the "ret" variable in our C++ code example.
It is not a simple job to figure out what a sequence of assembly instructions does, but a general idea of the mapping between the source code and instructions can be gained by observing the following points:
- Constant values in code can be directly recognized in the assembly.
- Arithmetic operations such as add, sub, imul, idiv, and many others can be recognized.
- Conditional jumps map to loops and conditionals.
- Function calls can be directly read (the function name appears in the assembly code).
Now, let's observe the effect of the code if we add a compiler flag for optimization in the compiler options field at the top-right:
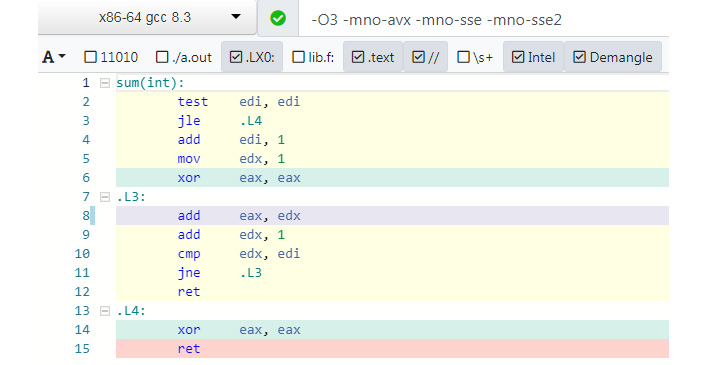
Figure 8.8: Adding a compiler flag for optimization
In the preceding screenshot, O3 stands for maximum optimization. The other flags, such as -mno-avx, -mno-sse, and -mno-sse2, are used to prevent the compiler from generating vector instructions that are not relevant to the current example. We can see that the compiler is no longer accessing memory and only working with registers. Notice the line xor eax, eax, which has an effect of storing 0 in eax—this is more efficient than loading a constant 0 from memory into the register. Since memory takes several clock cycles to access (anywhere from 5 to 100 clock cycles), using registers alone will itself produce a massive speedup.
When the compiler in the dropdown is changed to x86-64 clang 8.0.0, the assembly code is changed, which can be seen in the following screenshot:
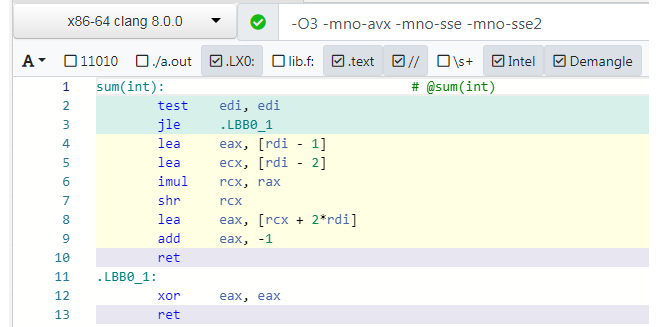
Figure 8.9: Assembly code with the new compiler
In the preceding assembly listing, observe that there is no instruction starting with J (for jump). Thus, there is no looping construct at all! Let's examine how the compiler is calculating the sum of 1 to n. If the value of n is <= 0, then it jumps to the.LBB0_1 label where it exits, returning 0. Let's analyze the following instructions:

Figure 8.10: Assembly code with the new compiler
The following code is the C equivalent of the previous instructions. Remember that n is in the EDI register (and hence also in the RDI register, since they overlap):
eax = n - 1;
ecx = n - 2;
rcx *= rax;
rcx >>= 1;
eax = rcx + 2 * n;
eax--;
return eax;
Alternatively, if we were to write it in one line, it would look like this:
return ((n-1) * (n-2) / 2) + (n * 2) - 1;
If we simplify this expression, we get the following:
((n^2 - 3n + 2) / 2) + 2n - 1
Alternatively, we can write it in the following format:
((n^2 - 3n + 2) + 4n - 2) / 2
This can be simplified to the following:
(n^2 + n) / 2
Alternatively, we can write the following:
(n * (n+1)) / 2
This is the closed form equation for the summation of numbers 1 to n inclusive, and the fastest way to compute it. The compiler was extremely clever—rather than just looking at our code line by line, it reasoned that the effect of our loop was to calculate the sum, and it figured out the algebra on its own. It did not figure out the simplest possible expression, but an equivalent one that took a few extra operations. Nevertheless, taking out the loop makes this function very much optimal.
If we modify the initial or final values of the i variable in the for loop to create a different summation, the compiler is still able to perform the necessary algebraic manipulation to derive a closed form solution needing no loops.
This is just one example of how compilers have become extremely efficient and appear almost intelligent. However, we must understand that this particular optimization of summations has been specifically programmed into the clang compiler. It does not mean that the compiler can do this kind of trick for any possible loop computation — that would actually require the compiler to have general artificial intelligence, as well as all the mathematical knowledge in the world.
Let's explore another example of compiler optimization via generated assembly code. Look at the following code:
#include <vector>
int three()
{
const std::vector<int> v = {1, 2};
return v[0] + v[1];
}
In the compiler options, if we select the x86-64 clang 8.0.0 compiler and add -O3 -stdlib=libc++, the following assembly code is generated:
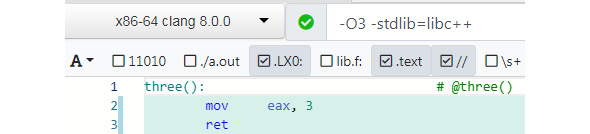
Figure 8.11: Assembly code generated with the new compiler
As you can see in the preceding screenshot, the compiler decided correctly that the vector was not relevant to the function and removed all the baggage. It also did the addition at compile time and directly used the result, 3, as a constant. The main things to take forward from this section are as follows:
- Compilers can be extremely clever when optimizing code, given the right options.
- Studying generated assembly code is very useful to get a high-level estimate of execution complexity.
- A basic understanding of how machine code works is valuable for any C++ programmer.
In the next section, we'll learn about manual execution timing.
Manual Execution Timing
This is the easiest way to quickly time small programs. We can use a command-line tool to measure the time taken for a program to execute. On Windows 7 and above, the following PowerShell command can be used:
powershell -Command "Measure-Command {<your program and arguments here>}"
On Linux, MacOS, and other UNIX-like systems, the time command can be used:
time <your program and arguments here>
In the next section, we'll implement a small program and examine some caveats about timing a program's execution in general.
Exercise 1: Timing a Program's Execution
In this exercise, we will write a program that performs a summation of an array. The idea here is to time the summation function. This method is useful when we wish to test a function written in isolation. Thus, the test program's only purpose is to execute one single function. Since the calculation is very simple, we will need to run the function thousands of times in order to get a measurable execution time. In this case, we'll just call the sumVector() function from the main() function, passing an std::vector of random integers.
Note
A program that's meant to test a single function is sometimes referred to as a driver program (not to be confused with a device driver).
Perform the following steps to complete this exercise:
- Create a file named Snippet1.cpp.
- Define a function named sumVector that sums up each element in a loop:
int sumVector(std::vector<int> &v)
{
int ret = 0;
for(int i: v)
{
ret += i;
}
return ret;
}
- Define the main function. Use the C++11 random number generation facilities to initialize a vector of 10,000 elements and then call the sumVector function 1,000 times. Write the following code to implement this:
#include <random>
#include <iostream>
int main()
{
// Initialize a random number generator
std::random_device dev;
std::mt19937 rng(dev());
// Create a distribution range from 0 to 1000
std::uniform_int_distribution<std::mt19937::result_type> dist(0,1000);
// Fill 10000 numbers in a vector
std::vector<int> v;
v.reserve(10000);
for(int i = 0; i < 10000; ++i)
{
v.push_back(dist(rng));
}
// Call out function 1000 times, accumulating to a total sum
double total = 0.0;
for(int i = 0; i < 1000; ++i)
{
total += sumVector(v);
}
std::cout << "Total: " << total << std::endl;
}
- Compile, run, and time this program on a Linux Terminal using the following commands:
$ g++ Snippet1.cpp
$ time ./a.out
The output of the previous command is as follows:

Figure 8.12: Output of timing the Snippet1.cpp code
As you can see from the preceding output, for this system, the program executed in 0.122 seconds (note that the results will vary, depending on your system's configuration). If we run this timing command repeatedly, we may get slight variations in the results as the program will be loaded in the memory after the first run and will be marginally faster. It is best to run and time the program about 5 times and get an average value. We are usually not interested in the absolute value of the time taken, but rather how the value improves as we optimize our code.
- Use the following commands to explore the effect of using compiler optimization flags:
$ g++ -O3 Snippet1.cpp
$ time ./a.out
The output is as follows:

Figure 8.13: Output of timing the Snippet1.cpp code compiled with -O3
From the preceding output, it seems that the program has become about 60 times faster, which seems quite unbelievable.
- Change the code to execute the loop 100,000 times rather than 1,000 times:
// Call out function 100000 times
for(int i = 0; i < 100000; ++i)
{
total += sumVector(v);
}
- Recompile and time again using the following commands:
$ g++ -O3 Snippet1.cpp
$ time ./a.out
The output after executing previous command is as follows:

Figure 8.14: Output of timing the Snippet1.cpp code with 10,000 iterations
From the preceding output, it still seems to take the exact same time. This seems impossibe, but actually what happens is that since we never caused any side effect in our program, such as printing the sum, the compiler is free to replace our code with an empty program. Functionally, according to the C++ standard, this program and an empty program are identical because there are no side effects of running it.
- Open the Compiler Explorer and paste in the entire code. Set the compiler options to -O3 and observe the generated code:

Figure 8.15: Snippet1.cpp code in Compiler Explorer
As you can see from the preceding screenshot, the lines within the for loop are not color-coded and no assembly code was generated for them.
- Change the code to make sure that the sum must be performed by printing a value that depends on the computation with the following line:
std::cout<<"Total:"<<total<<std::endl;
- Here, we are just summing the result of sumVector() to a dummy double value many time and printing it. After you make the changes in the code, open the Terminal and write the following commands:
$ g++ -O3 Snippet1.cpp
$ time ./a.out
The output of the previous commands is as follows:

Figure 8.16: Output of timing the Snippet1.cpp code with a side effect of printing the value
In the preceding output, we can see that the program actually performed the computation instead of just running as an empty program. Printing the total to cout is a side effect that causes the compiler not to elide the code. Causing a side effect (such as printing a result) that depends on the code's execution is one way to prevent the compiler optimizer from removing code. In the next section, we'll learn how to time programs without side effects.
Timing Programs without Side Effects
As seen in the previous exercise, we needed to create a side effect (using cout) in our program so that the compiler did not ignore all the code we wrote. Another technique to make the compiler believe that a piece of code has a side effect is to assign its result to a volatile variable. The volatile qualifier tells the compiler: "This variable must always be read from memory and written to memory, and not from a register." The main purpose of a volatile variable is to access device memory, and such device memory access must follow the rule mentioned above. Effectively, volatile variables are considered by the compiler as if they could change from effects outside of the current program, and thus will never be optimized. We will use this technique in the upcoming sections.
There are more advanced ways to bypass this problem, that is, by specifying special assembly code directives to the compiler rather than using side effects. But they are outside the scope of this introductory material. For the examples that follow, we'll always add code that ensures that a function's result is used in a side effect or is assigned to a volatile variable. In future sections, we'll learn how to examine the compiler generated assembly code and detect instances when the compiler elides code for optimization purposes.
Source Code Instrumentation
Instrumentation is a term that refers to the process of adding extra code to a program, without changing its behavior, and capturing the information as it executes. This may include performance timing (and possibly other measurements such as memory allocation, or disk usage patterns). In the case of source code instrumentation, we manually add code to time the execution of our program and log that data when the program ends, for analysis. The advantage of this approach is its portability and avoidance of any external tools. It also allows us to selectively add the timing to any part of the code we choose.
Exercise 2: Writing a Code Timer Class
In this exercise, we'll create an RAII class that allows us to measure the execution time of individual blocks of code. We will use this as the primary timing mechanism for the code in the exercises that follow. It is not as sophisticated as other methods of performance measurement but is much easier to use and serves most purposes. The basic requirement of our class is as follows:
- We need to be able to record the cumulative time taken by a block of code.
- We need to be able to record the number of times it is invoked.
Perform the following steps to complete this exercise:
- Create a file named Snippet2.cpp.
- Include the following headers:
#include <map>
#include <string>
#include <chrono>
#include <iostream>
#include <cstdint>
using std::map;
using std::string;
using std::cerr;
using std::endl;
- Define the Timer class and the class member functions by writing the following code:
class Timer
{
static map<string, int64_t> ms_Counts;
static map<string, int64_t> ms_Times;
const string &m_sName;
std::chrono::time_point<std::chrono::high_resolution_clock> m_tmStart;
As you can see from the preceding code, the class members consist of a name, a starting timestamp, and two static maps. Every instance of this class is meant to time a certain block of code. The block can be a function scope or any other block delimited by curly braces. The usage pattern is to define an instance of the Timer class at the top of the block while passing in a name (can be a function name or some other convenient label). When instantiated, the current timestamp is recorded, and when the block exits, the destructor of this class records the cumulative time elapsed for this block, as well as the count of the number of times this block executed. The times and counts are stored in the static maps ms_Times and ms_Counts, respectively.
- Define the constructor of the Timer class by writing the following code:
public:
// When constructed, save the name and current clock time
Timer(const string &sName): m_sName(sName)
{
m_tmStart = std::chrono::high_resolution_clock::now();
}
- Define the destructor of the Timer class by writing the following code:
// When destroyed, add the time elapsed and also increment the count under this name
~Timer()
{
auto tmNow = std::chrono::high_resolution_clock::now();
auto msElapsed = std::chrono::duration_cast<std::chrono::milliseconds>(tmNow - m_tmStart);
ms_Counts[m_sName]++;
ms_Times[m_sName] += msElapsed.count();
}
In the preceding code, the elapsed time is calculated in milliseconds. Then, we add that to the cumulative elapsed time for this block name and increment the count of how many times this block was executed.
- Define a static function named dump() that prints out the summary of the timed results:
// Print out the stats for each measured block/function
static void dump()
{
cerr << "Name\t\t\tCount\t\t\tTime(ms)\t\tAverage(ms)\n";
cerr << "-----------------------------------------------------------------------------------\n";
for(const auto& it: ms_Times)
{
auto iCount = ms_Counts[it.first];
cerr << it.first << "\t\t\t" << iCount << "\t\t\t" << it.second << "\t\t\t" << it.second / iCount << "\n";
}
}
};
In the preceding code, the name, execution count, total time, and average time is printed in a tabular form. We use multiple tabs between the field names and field values to make them line up vertically on a console. This function can be modified as we wish. For example, we can modify this code to dump the output as a CSV file, so that it can be imported into a spreadsheet for further analysis.
- Finally, define the static members to complete the class:
// Define static members
map<string, int64_t> Timer::ms_Counts;
map<string, int64_t> Timer::ms_Times;
const int64_t N = 1'000'000'000;
- Now that we have defined the Timer class, define two simple functions that we will time as an example. One will add and the other will multiply. Since these operations are trivial, we will loop 1 billion times so that we can have some measurable result.
Note
C++ 14 and above let us use the single-quote symbol within integer constants for readability; for example, we can write 1'000'000 rather than 1000000.
Write the functions for addition and multiplication. Both functions simply add and multiply the integers 1 to N, respectively:
unsigned int testMul()
{
Timer t("Mul");
unsigned int x = 1;
for(int i = 0; i < N; ++i)
{
x *= i;
}
return x;
}
unsigned int testAdd()
{
Timer t("Add");
unsigned int x = 1;
for(int i = 0; i < N; ++i)
{
x += i;
}
return x;
}
In the preceding code, we used unsigned int for the variable that we repeatedly add/multiply. We used an unsigned type so that overflow during arithmetic does not result in undefined behavior. Had we used a signed type, the program would have undefined behavior and not be guaranteed to work in any way. Secondly, we return the calculated value from the testAdd() and testMul() functions so that we can ensure that the compiler does not remove the code (because of the lack of side effects). In order to time each of these functions, we need to simply declare an instance of a Timer class with a suitable label at the start of the function. The timing is started as soon as the Timer object is instantiated and stopped when that object goes out of scope.
- Write the main function, where we will simply call both test functions 10 times each:
int main()
{
volatile unsigned int dummy;
for(int i = 0; i < 10; ++i)
dummy = testAdd();
for(int i = 0; i < 10; ++i)
dummy = testMul();
Timer::dump();
}
As you can see in the preceding code, we're calling each function 10 times so that we can demonstrate the Timer class timing multiple runs of a function. Assigning the result of the functions to a volatile variable forces the compiler to assume that there is a global side effect. Hence, it will not elide the code in our test functions. Before exiting, we call the Timer::dump static function to display the results.
- Save the program and open a terminal. Compile and run the program with different optimization levels – on the gcc and clang compilers, this is specified by the -ON compiler flag, where N is a number from 1 to 3. Add the -O1 compiler flag first:
$ g++ -O1 Snippet2.cpp && ./a.out
This code generates the following output:

Figure 8.17: Snippet2.cpp code performance when compiled with the -O1 option
- Now, add the -O2 compiler flag in the terminal and execute the program:
$ g++ -O2 Snippet2.cpp && ./a.out
This generates the following output:

Figure 8.18: Snippet2.cpp code performance when compiled with the -O2 option
- Add the -O3 compiler flag in the terminal and execute the program:
$ g++ -O3 Snippet2.cpp && ./a.out
This generates the following output:

Figure 8.19: Snippet2.cpp code performance when compiled with the -O3 option
Notice that the testMul function became faster only at O3, but the testAdd function got faster at O2 and much faster at O3. We can verify this by running the program multiple times and averaging the times. There are no obvious reasons why some functions speed up while others do not. We would have to exhaustively check the generated code to understand why. It is not guaranteed that this will happen on all the systems with different compilers or even compiler versions. The main point to take home is that we can never assume performance but have to always measure it, and always re-measure if we believe any change we made affects the performance.
- To make it easier to use our Timer class for timing individual functions, we can write a macro. C++ 11 and above support a special compiler built-in macro called __func__ that always contains the currently executing function's name as a const char*. Use this to define a macro so that we don't need to specify a label for our Timer instances, as follows:
#define TIME_IT Timer t(__func__)
- Add the TIME_IT macro to the start of the two functions, changing the existing line that creates a Timer object:
unsigned int testMul()
{
TIME_IT;
unsigned int testAdd()
{
TIME_IT;
- Save the program and open the terminal. Compile and run it again by using the following command:
$ g++ -O3 Snippet2.cpp && ./a.out
The output of the previous command is as follows:

Figure 8.20: Snippet2.cpp code output when using a macro for timing
In the preceding output, notice that the actual function name is printed now. Another advantage of using this macro is that we can add this to all potentially time-consuming functions by default, and disable it for production builds by simply changing the definition to a no-op, which will cause the timing code to never run - avoiding the need to edit the code extensively. We will use this same Timer class for timing code in forthcoming exercises.



























































