Project 7 – Using the temperature sensor
The Nexys A7 board has an Analog Device ADT7420 temperature sensor. This chip uses an industry-standard I2C interface to communicate. This two-wire interface is used primarily for slower-speed devices. It has the advantage of allowing multiple chips to be connected through the same interface and be addressed individually. In our case, we will be using it to simply read the current temperature from the device and display the value on the seven-segment display.
Our first step will be to design an I2C interface. In Chapter 8, Introduction to AXI, we’ll be looking at designing a general-purpose I2C interface, but for now, we’ll use the fact that the ADT7420 comes up in a mode where we can get temperature data by reading two I2C memory locations. First, let’s look at the timing diagram for the I2C bus and the read cycle we’ll be using:
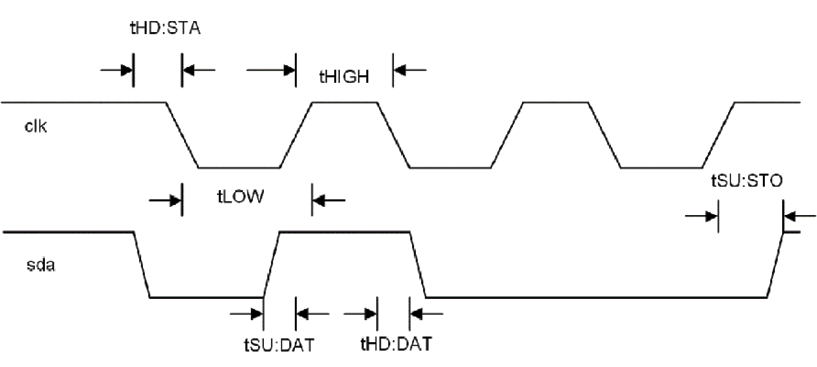
Figure 6.13: I2C timing
We can see from the timing diagram...


























































