Bayes' theorem
Bayes' theorem is a formula for calculating the probability of an event using prior knowledge of related conditions. The theorem was discovered by an English statistician and minister named Thomas Bayes in the 18th century. Bayes never published his work; his notes were edited and published posthumously by the mathematician Richard Price. Bayes' theorem is given by the following formula:
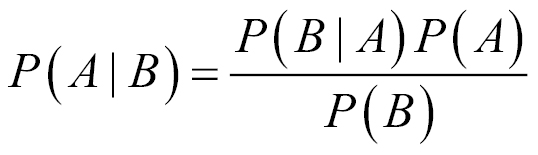
A and B are events; P(A) is the probability of observing event A, and P(B) is the probability of observing event B. P(A|B) is the conditional probability of observing A given that B was observed. In classification tasks, our goal is to map features of explanatory variables to a discrete response variable; we must find the most likely label, A, given the features, B.
Note
A theorem is a mathematical statement that has been proven to be true based on axioms or other theorems.
Let's work through an example. Assume that a patient exhibits a symptom of a particular disease, and that a doctor administers...












































































