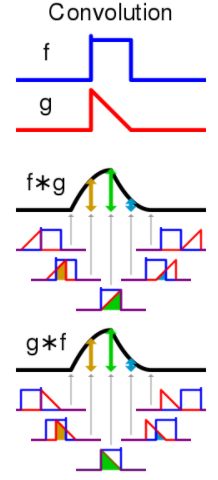
The word convolvere comes from Latin and translates to convolve or roll together. From a mathematical perspective, you may define a convolution as the calculus-based integral denoting the amount by which two given functions overlap, as one of the two is slid across the other. In other words, performing the convolution operation on two functions (f and g) will produce a third function that expresses how the shape of one is modified by the other. The term convolution refers to both the result function and the computation process, with roots in the mathematical subfield of signal processing, as we can here in this diagram:
So, how can we leverage this operation to our advantage?


























































