Closest point triangle
To find the closest point on a triangle to a test point, we must first create a plane out of the triangle. Three points that are not in a straight line are coplanar. This means we can create a plane out of any triangle. Once we have a plane, we get the closest point on the plane to the test point. Next, we check if this new closest point is inside the triangle. If it is, we return it as the closest point on the triangle.
If the closest point was not contained within the triangle, it's going to be on one of the triangle edges. We must construct a line out of each triangle edge and find the closest point on each line to the test point. We then return the closest point to the test point of the three closest points from the last step:
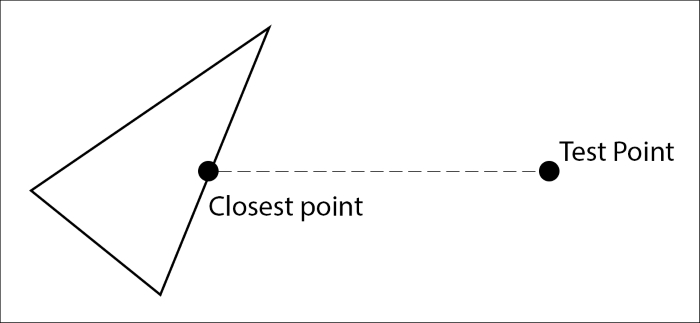
If a test point is outside of the triangle, the closest point is going to be on one of the edge lines of the triangle. We can calculate this closest point using the closest point to line formula.
Getting ready
Before implementing the ClosestPoint...




























































