What is a linear transformation?
To be precise, a linear transformation is a function T from a vector space U to a vector space V. A capital letter "T" is traditionally used by mathematicians to denote a generic transformation, and we use the same syntax that we introduced for functions in Anchor 3, Foundations:
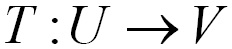
Similarly, the vector space U is the domain, and the vector space V is the codomain. Each vector that is transformed is called the image of the original vector in the domain. The set of all images is the range.
To be linear, the transformation must preserve the operations of vector addition and scalar multiplication by meeting the conditions for linearity. Here, we express them in terms of vectors:
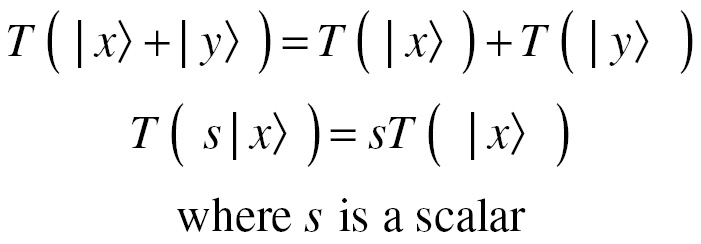
It follows from these axioms that for any linear transformation T, T (0) has to equal the zero vector 0. Let's look at how we describe transformations in the next section.






















































