1.1 Linear Algebra for Quantum Mechanics
Quantum computing and quantum mechanics rely on a specific notational formalism, due to Dirac, and are supported by classical linear algebra, in particular Hermitian structures of matrices and tensor products. We provide here a self-contained review of these tools to facilitate the understanding of the rest of the book. We start with basic linear algebra principles before introducing Dirac notations and the quantum counterparts of linear algebra tools. Sections 1.1.1 to 1.1.4 concentrate on standard definitions of finite-dimensional Hilbert spaces and matrices, while Sections 1.1.5 to 1.1.7 review the key details and properties of complex matrices (decompositions, Hermitian property, and rotations). Sections 1.1.9 to 1.1.11 introduce Dirac’s formalism and the essential aspects of quantum operators.
1.1.1 Basic definitions and notations
We let 𝔽 denote either the real field ℝ or the complex one ℂ. For a complex number z = x+iy ∈ℂ, with x,y ∈ℝ, we write the conjugate z∗ := x−iy. We let ℳm,n(𝔽) denote the space of matrices of dimension m × n with entries in 𝔽 and ℳn(𝔽) whenever m = n. For A := (aij)1≤i≤m; 1≤j≤n ∈ℳm,n(𝔽), A∗ := (aij∗)1≤i≤m; 1≤j≤n is the complex conjugate. If A ∈ℳn(𝔽), we write A⊤ for its transpose and A† := (A∗)⊤ for its Hermitian conjugate. We finally denote I the identity matrix and write In whenever we wish to emphasise the dimension, and 0m,n the null matrix in ℳm,n(𝔽). Recall that a matrix A ∈ℳn(𝔽) is invertible (or non-singular) if there exists B ∈ℳn(𝔽) such that AB = BA = In. Given two matrices A ∈ℳp,m(𝔽) and B ∈ℳq,n(𝔽), we define their tensor product as
Since a vector is a particular case of a matrix, for u ∈𝔽m and v ∈𝔽n, we can write
1.1.2 Inner products
A vector space V over the field 𝔽 is a set endowed with
- a commutative, associative addition operation,
- an operation of multiplication by a scalar.
The addition and the multiplication by a scalar have the following properties (for scalars α,β ∈𝔽 and vectors u,v ∈V):
- v + 0 = v;
- v + (−v) = 0;
- α(βv) = (αβ)v;
- (α + β)v = αv + βv;
- α(u + v) = αu + αv;
- 1 ⋅ v = v.
Armed with this, we can now define an inner product on V:
Definition 1. A map ⟨⋅,⋅⟩ : V ×V →𝔽 is called an inner product if, for u,v,w ∈V and α ∈𝔽,
- (Positive definiteness) ⟨u,u⟩≥ 0 and ⟨u,u⟩ = 0 if and only if u = 0;
- (Conjugate symmetry) ⟨u,v⟩ = ⟨v,u⟩∗;
- (Linear in the first argument) ⟨u + v,w⟩ = ⟨u,w⟩ + ⟨v,w⟩ and ⟨αu,v⟩ = α⟨u,v⟩;
- (Antilinear in the second argument) ⟨u,v + w⟩ = ⟨u,v⟩ + ⟨u,w⟩ and ⟨u,αv⟩ = α∗⟨u,v⟩.
The inner product is further called non-degenerate if ⟨u,v⟩ = 0 for all v ∈V ∖{0} implies u = 0.
For example, the following spaces carry a natural inner product:
- The vector space ℂn with the inner product ⟨u,v⟩ := u†v = ∑ i=1nui∗vi;
- The space of complex-valued continuous functions on [0,1] with ⟨f,g⟩ := ∫ 01f(t)∗g(t)dt;
- If X,Y ∈ℳm,n(ℝ), then ⟨X,Y⟩ := Tr(X⊤Y) = ∑ i=1m ∑ j=1nXijYij defines an inner product on the space of (real) matrices.
Projection matrices are particularly useful for geometric purposes:
Definition 2. A matrix P ∈ℳn(𝔽) is called a (orthogonal) projection if P2 = P.
In particular, if W is a vector subspace of 𝔽n with some orthonormal basis (w1,…,wd), it is then easy to check that the map 𝒫W : 𝔽n →𝔽n onto W satisfying
defines an orthogonal projection.
1.1.3 From linear operators to matrices
Let V be a finite-dimensional vector space over 𝔽 and ⟨⋅,⋅⟩ a non-degenerate inner product on V. Given a linear operator 𝒜 : V →V, then, by the Riesz representation theorem [309, Section III-6], there exists a unique linear operator 𝒜† : V →V, called the adjoint operator, such that
Indeed, for any v ∈V, the map u ∈V ⟨𝒜u,v⟩ is a linear functional, hence an element of the dual space V† (the space of bounded linear functionals on V), therefore for each v ∈V, there exists v′∈V such that ⟨𝒜u,v⟩ = ⟨u,v′⟩. It is then easy to show that the map v
⟨𝒜u,v⟩ is a linear functional, hence an element of the dual space V† (the space of bounded linear functionals on V), therefore for each v ∈V, there exists v′∈V such that ⟨𝒜u,v⟩ = ⟨u,v′⟩. It is then easy to show that the map v v′ is linear, proving that the adjoint operator is uniquely defined. In the particular case where 𝒜 = 𝒜†, the operator 𝒜 is called Hermitian, a key requirement in quantum mechanics:
v′ is linear, proving that the adjoint operator is uniquely defined. In the particular case where 𝒜 = 𝒜†, the operator 𝒜 is called Hermitian, a key requirement in quantum mechanics:
Definition 3. The operator 𝒜 is called Hermitian, or self-adjoint, if 𝒜 = 𝒜†.
For a Hermitian operator 𝒜, we then have, for any u ∈V,
by conjugate symmetry (Definition 1), and therefore ⟨𝒜u,u⟩ is real. Conversely, if ⟨𝒜u,u⟩ is real, then
Therefore,  = 0; since this is true for all u ∈V, then 𝒜 = 𝒜†.
= 0; since this is true for all u ∈V, then 𝒜 = 𝒜†.
The following property of operators shall be useful to ensure that systems driven by operators preserve distances, or norms:
Definition 4. The linear operator 𝒜 : V → V is called unitary if it is surjective and
Recall that a linear operator between two finite-dimensional normed spaces is bounded, and therefore continuous. For any u ∈V, this implies that ∥𝒜u∥ = ∥u∥, so that a unitary operator 𝒜 preserves the norm. In that case, 𝒜 is an isometry, therefore injective. Being also surjective, it is bijective and therefore its inverse exists. For a unitary operator 𝒜 and any u,v ∈V, we have
by definition of the adjoint, implying that
where ℐ is the identity operator.
Example (Real Matrices): If V = ℝn with inner product ⟨u,v⟩ := u⊤v for u,v ∈ℝn, the linear operator 𝒜 can now be viewed as a matrix A in ℳn(ℝ). Its adjoint is nothing other than the transpose A⊤, and therefore A is self-adjoint if and only if it is symmetric. In this case, if A is unitary (or orthogonal), then it is invertible with A−1 = A⊤. Rotation matrices in ℝ2, which will play an important role later when constructing quantum circuits, are the only unitary maps of ℝ2 onto itself and are of the form
for 𝜃 ∈ [0,2π) and δ ∈{−1,+1}.
Example (Complex Matrices): If V = ℂn with inner product ⟨u,v⟩ := v†u for u,v ∈ℂn, the linear operator 𝒜 can now be viewed as a matrix in ℳn(ℂ). The adjoint of such a matrix is then the Hermitian conjugate A† and A is called Hermitian if A = A† and unitary if A†A = In. We shall denote by 𝒰n(ℂ) the set of unitary matrices in ℳn(ℂ). We will discuss Hermitian matrices over ℂ in more detail in Section 1.1.6.
1.1.4 Condition number
In order to manipulate matrices and measure them, we require matrix norms:
Definition 5. A matrix norm ∥⋅∥ : ℳm,n(𝔽) →ℝ is a function satisfying, for any α ∈𝔽 and A,B ∈ℳm,n(𝔽),
- (positively valued) ∥A∥≥ 0;
- (definite) ∥A∥ = 0 if and only if A = 0m,n;
- (absolutely homogeneous) ∥αA∥ = |α|∥A∥;
- (triangle inequality) ∥A + B∥≤∥A∥ + ∥B∥.
The norm is further called sub-multiplicative if ∥AB∥≤∥A∥∥B∥.
The condition number of a matrix is an important tool to understand the stability of linear equations of the form Ax = b, for A ∈ℳn(𝔽), b ∈𝔽n. Assuming A to be non-singular, the true solution is clearly x∗ := A−1b. Suppose, however, that the vector b is only known up to some (not necessarily quantum) measurement error, and one observes instead b + Δb. The solution is then A−1(b + Δb) = x∗ + Δx, with Δx := A−1Δb. In particular, we can write, for any (sub-multiplicative) matrix norm ∥⋅∥,
From this inequality, we see that the quantity ∥A−1∥∥A∥ bounds the relative error in the solution with respect to the relative error in the measurement of the input vector b. This leads to the following terminology:
Definition 6. Given a matrix A ∈ ℳn(𝔽) and a sub-multiplicative norm ∥⋅∥, we call
the condition number (with respect to the norm ∥⋅∥) of the matrix A (and assign to it infinite value if A is singular).
Remark: The definition of the condition number above holds for any matrix norm ∥⋅∥, but admits a more explicit representation in the particular case of the spectral norm ∥⋅∥2, defined as
where ∥x∥2 := 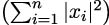
 is the L 2 norm for vectors. If the matrix A is not singular, then
is the L 2 norm for vectors. If the matrix A is not singular, then
where λmax(A) and λmin(A) denote the largest and smallest eigenvalues of A.
1.1.5 Matrix decompositions and spectral theorem
Having defined essential properties of (complex) matrices, we now introduce several essential tools that allow us to gain a better understanding of their properties.
The Singular Value Decomposition is a key tool to analyse the properties and behaviours of matrices. It is ubiquitous in applied statistics and machine learning and allows us to reduce the explanatory dimension of a large matrix into a small number of meaningful components.
Theorem 1 (Singular Value Decomposition). Let A ∈ℳm,n(𝔽) and p := min(m,n). There exist U ∈𝒰m(𝔽), V ∈𝒰n(𝔽) and σ1 ≥ ≥ σp ≥ 0 such that A = UΣV†, where Σ ∈ℳm,n(𝔽) is diagonal with Σii = σi for i = 1,…,p and Σii = 0 for i > p.
≥ σp ≥ 0 such that A = UΣV†, where Σ ∈ℳm,n(𝔽) is diagonal with Σii = σi for i = 1,…,p and Σii = 0 for i > p.
The numbers {σ1,…,σp} are called the singular values of A and are uniquely defined. The columns of U and V are the left-singular and right-singular vectors of A, in the sense that, if σ ∈{σ1,…,σp}, then there exist a column u of U and a column v of V such that Av = σu and A†u = σv. Recall that the rank of a matrix is defined as the dimension of the span of its columns. As a corollary of the Singular Value Decomposition theorem, the rank of a matrix is therefore equal to the number of non-zero singular values. The Singular Value Decomposition is general in the sense that it holds for any matrix. In the particular case of square matrices, the Schur decomposition and the Spectral Theorem provide refinements.
The Spectral Theorem is a cornerstone result in the theory of linear operators, and in particular for (finite-dimensional) matrices. Recall that an operator 𝒜 : V →V is called normal if it commutes with its adjoint, namely if 𝒜𝒜† = 𝒜†𝒜. Self-adjoint (or Hermitian) operators are clearly normal, yet the converse is not true in general. Recall further that an eigenvector of 𝒜 is a non-zero vector u ∈V such that 𝒜u = λu for some λ ∈ℂ, and we denote by σ(𝒜) the set of eigenvalues of 𝒜.
The following result, which is more general than the subsequent spectral theorem, allows us to decompose any arbitrary complex square matrix.
Theorem 2 (Schur Decomposition). For any A ∈ ℳn(ℂ) there exits a unitary matrix U ∈ 𝒰n(ℂ) and an upper triangular matrix T such that A = UTU−1.
Note that since U is unitary, then U−1 = U†. We call the matrix T the Schur transform of A and the identity in the theorem means that A and T are similar, so in particular, possess the same eigenvalues, all located on the diagonal of T. If A is a normal matrix, then so is T, and therefore T must be diagonal and we write T = D for clarity. In this case, we say that the matrix A is diagonalisable with A = UDU†, where the diagonal entries of D are the eigenvalues of A and the column vectors of U are the orthonormal eigenvectors of A.
Theorem 3 (Spectral Theorem). The linear operator 𝒜 : V → V is normal if and only if there exists an orthonormal basis of V consisting of eigenvectors of A.
For each eigenvalue λ ∈ σ(𝒜), denote the corresponding eigenspace
Since the vector space V is the orthogonal direct sum of the eigenspaces (indexed by the eigenvalues of 𝒜), we can then write the spectral decomposition
where 𝒫λ is the orthogonal projection operator onto 𝒱λ. Note that such an operator is naturally self-adjoint [309, Theorem 2, Section III-1].
1.1.6 Hermitian matrices
We introduced above Hermitian matrices as the set of matrices A over the complex field ℂ such that A = A†. As fundamental building blocks of quantum computing, we investigate their properties further. Clearly, a real matrix is Hermitian if and only if it is symmetric, in which case A⊤ = A.
Proposition 1. The eigenvalues of a Hermitian matrix are real.
Proof. If Ax = λx for λ ∈ℂ and x ∈ℂn, then
| ⟨Ax,x⟩ |
= x†Ax = λx†x = λ∥x∥2, |
| ⟨x,Ax⟩ |
= (Ax)†x = (λx)†x = λ∗x†x = λ∗∥x∥2. |
Since both are equal by the Hermitian property, then λ = λ∗, proving the proposition. □
The Singular Value Decomposition (Theorem 1) takes a particular flavour in the case of Hermitian matrices:
Theorem 4. With the notations of Theorem 1, if A ∈ ℳn(ℂ) is Hermitian, then the matrices U and V are equal and the matrix Σ is diagonal with real entries.
Theorem 5. For a Hermitian matrix A ∈ ℳn(ℂ), the following are equivalent:
-
The eigenvalues are non-negative.
-
There exists a Hermitian matrix B ∈ℳn(ℂ) such that A = B2.
-
There exists a matrix B ∈ℳn(ℂ) such that A = B†B.
-
For every x ∈ℂn, ⟨Ax,x⟩≥ 0.
Such a matrix is called positive semi-definite.
Proof. The Spectral Theorem shows that there exist a unitary matrix U ∈𝒰n(ℂ) and a diagonal matrix Σ ∈ℳn(ℂ) such that A = UΣU†, where the diagonal elements of Σ are the eigenvalues of A. Assuming (i), we can define B = U U†∈ℳn(ℂ). Then clearly
U†∈ℳn(ℂ). Then clearly
since U is unitary. The equality A = B†B is also obvious. The latter implies that
Finally, assume (iv) and let λ be an eigenvalue of A with eigenvector u. Then
Since the latter is strictly positive, then clearly λ ≥ 0.
The following property lies at the core of Hamiltonian simulation of quantum systems:
Theorem 6. If A ∈ ℳn(ℂ) is Hermitian, then, for any t ∈ ℝ, eitA is unitary; conversely, every unitary matrix has the form eitA for some Hermitian matrix A.
Recall that for a matrix A ∈ℳn(ℂ), its exponential is given by
In practice, though, given a Hermitian matrix A, finding the corresponding unitary matrix U is not easy. The Hamiltonian simulation problem is defined as follows.
Hamiltonian Problem: Given a Hermitian matrix A ∈ℳn(ℂ), a time t > 0, a tolerance level 𝜀 > 0, and some matrix norm ∥⋅∥, find a unitary matrix U such that  ≤ 𝜀.
≤ 𝜀.
1.1.7 Rotation matrices
Rotation matrices, and later their quantum gate equivalents will play a key role in building quantum circuits. Let us start with the following lemma:
Lemma 1. If a matrix A ∈ℳn(ℂ) is such that A2 = I, then for any 𝜃 ∈ℝ,
Proof. This follows directly from the series expansion
which has an infinite radius of convergence. □
Lemma 1 will prove essential for computational purposes. As simple examples, consider the following:
Exercise: Compute ei𝜃A for A ∈{X,Y,Z} and 𝜃 ∈ℝ, where
For any α ∈ [0,2π), consider now the map ℛα : ℝ2 →ℝ2 such that
which is basically a rotation of angle α and does not affect the norm of the input vector. To the map ℛα, we can associate the (rotation) matrix Rα such that ℛα(u) = Rαu for any u ∈ℝ2. It is easy (exercise) to show the following:
Lemma 2. The matrix Rα has the form
This representation is the general form of a rotation matrix in ℝ2 (introduced in (1.1.3)).
Exercise: Write the matrices ei𝜃A for A ∈{X,Y,Z} from the previous exercise as rotation matrices.
1.1.8 Polar coordinates
Recall that a point z = x + iy, with x,y ∈ℝ, lying on the unit circle can be written as z = ei𝜃 with 𝜃 ∈ [0,2π). Indeed, simply let x = r cos(𝜃), y = r sin(𝜃) and add the constraint r = 1. Consider now a general vector u ∈ℂ2 of the form
with α,β ∈ℂ such that |α|2 + |β|2 = 1. Here, (e1,e2) forms a basis of ℝ2:
In polar coordinates, we can then write
Note that arbitrary multiplication phases have no influence – a fact of key importance in quantum mechanics – because, for any γ ∈ℝ,
so that in fact, multiplying u by the global phase e−i𝜃α and letting 𝜃 := 𝜃β −𝜃α, we consider
Write temporarily rβei𝜃 = x + iy. Insisting on u being on the unit sphere further imposes ∥u∥2 = 1, namely
| 1 |
= ∥u∥2 =  rαe1 + (x + iy)e2 rαe1 + (x + iy)e2 † † rαe1 + (x + iy)e2 rαe1 + (x + iy)e2 |
|
=  rαe1⊤ + (x − iy)e 2⊤ rαe1⊤ + (x − iy)e 2⊤  rαe1 + (x + iy)e2 rαe1 + (x + iy)e2 |
|
= rα2 + x2 + y2, |
since (e1,e2) is orthonormal. This is nothing more than the equation of the unit sphere. In polar coordinates, we can write
and clearly r = 1 since we are on the unit sphere. Therefore
| u |
= cos(𝜃)e1 +  sin(𝜃)cos(ϕ) + isin(𝜃)sin(ϕ) sin(𝜃)cos(ϕ) + isin(𝜃)sin(ϕ) e2 e2 |
|
= cos(𝜃)e1 + sin(𝜃)eiϕe 2. |
1.1.9 Dirac notations
Given a vector v ∈ℂn, Dirac’s ket and bra notations read
With these notations, the operation  := ⟨u|v⟩ defines an inner product on ℂn. The notation for the standard orthonormal basis in ℂn is (
:= ⟨u|v⟩ defines an inner product on ℂn. The notation for the standard orthonormal basis in ℂn is ( )i=0,…,n−1, i.e.,
)i=0,…,n−1, i.e.,
In coordinates, we can write, for any u,v ∈ℂn,
and therefore,
1.1.10 Quantum operators
In the language of Dirac’s notations, we can define the outer product  ⟨v| (for u ∈U and v ∈V) as a linear operator from V to U, two vector spaces, as
⟨v| (for u ∈U and v ∈V) as a linear operator from V to U, two vector spaces, as
In particular,  ⟨v| is the projection on the one-dimensional space generated by
⟨v| is the projection on the one-dimensional space generated by  . Any linear operator can be expressed as a linear combination of outer products as
. Any linear operator can be expressed as a linear combination of outer products as
where  and
and  are the standard basis vectors (1.1.9).
are the standard basis vectors (1.1.9).
Similarly to the linear algebra setting above, we can define an eigenvector of a linear operator 𝒜 : V →V as a non-zero vector  such that
such that
for some complex eigenvalue λ. Associated with any linear operator 𝒜, the adjoint operator 𝒜† satisfies
Indeed, in the language of linear operators above, we have
by definition of the inner product (Definition 1).
 United States
United States
 Great Britain
Great Britain
 India
India
 Germany
Germany
 France
France
 Canada
Canada
 Russia
Russia
 Spain
Spain
 Brazil
Brazil
 Australia
Australia
 Singapore
Singapore
 Hungary
Hungary
 Ukraine
Ukraine
 Luxembourg
Luxembourg
 Estonia
Estonia
 Lithuania
Lithuania
 South Korea
South Korea
 Turkey
Turkey
 Switzerland
Switzerland
 Colombia
Colombia
 Taiwan
Taiwan
 Chile
Chile
 Norway
Norway
 Ecuador
Ecuador
 Indonesia
Indonesia
 New Zealand
New Zealand
 Cyprus
Cyprus
 Denmark
Denmark
 Finland
Finland
 Poland
Poland
 Malta
Malta
 Czechia
Czechia
 Austria
Austria
 Sweden
Sweden
 Italy
Italy
 Egypt
Egypt
 Belgium
Belgium
 Portugal
Portugal
 Slovenia
Slovenia
 Ireland
Ireland
 Romania
Romania
 Greece
Greece
 Argentina
Argentina
 Netherlands
Netherlands
 Bulgaria
Bulgaria
 Latvia
Latvia
 South Africa
South Africa
 Malaysia
Malaysia
 Japan
Japan
 Slovakia
Slovakia
 Philippines
Philippines
 Mexico
Mexico
 Thailand
Thailand


















