Lattices in options pricing
In binomial trees, each node recombines at every alternative node. In trinomial trees, each node recombines at every other node. This property of recombining trees can also be represented as lattices to help you save memory without recomputing and storing recombined nodes.
Using a binomial lattice
We will create a binomial lattice from the binomial CRR tree since, at every alternate up and down nodes, the prices recombine to the same probability of  . In the following figure,
. In the following figure,  and
and  recombine with
recombine with  . The tree can now be represented as a single list:
. The tree can now be represented as a single list:
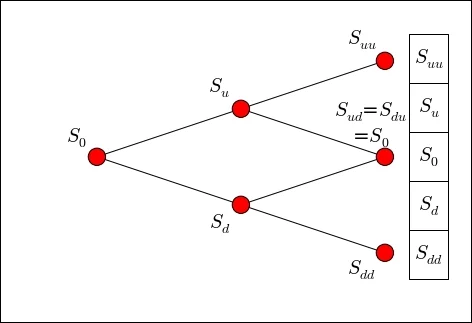
For a N-step binomial, a list of size  is required to contain the information on the underlying stock prices. For European option pricing, the odd nodes of payoffs from the list represent the option value upon maturity. The tree traverses backward to obtain the option value. For American option pricing, as the tree traverses backward, both ends of the list shrink, and the odd nodes represent the associated stock prices for...
is required to contain the information on the underlying stock prices. For European option pricing, the odd nodes of payoffs from the list represent the option value upon maturity. The tree traverses backward to obtain the option value. For American option pricing, as the tree traverses backward, both ends of the list shrink, and the odd nodes represent the associated stock prices for...






















































