Functions and automatic differentiation
The previous section introduced the function instruction to compile the expression. In this section, we develop some of the following arguments in its signature:
def theano.function(inputs, outputs=None, updates=None, givens=None, allow_input_downcast=None, mode=None, profile=None, )
We've already used the allow_input_downcast feature to convert data from float64 to float32, int64 to int32 and so on. The mode
and profile
features are also displayed because they'll be presented in the optimization and debugging section.
Input variables of a Theano function should be contained in a list, even when there is a single input.
For outputs, it is possible to use a list in the case of multiple outputs to be computed in parallel:
>>> a = T.matrix()
>>> ex = theano.function([a],[T.exp(a),T.log(a),a**2])
>>> ex(numpy.random.randn(3,3).astype(theano.config.floatX))
[array([[ 2.33447003, 0.30287042, 0.63557744],
[ 0.18511547, 1.34327984, 0.42203984],
[ 0.87083125, 5.01169062, 6.88732481]], dtype=float32),
array([[-0.16512829, nan, nan],
[ nan, -1.2203927 , nan],
[ nan, 0.47733498, 0.65735561]], dtype=float32),
array([[ 0.71873927, 1.42671108, 0.20540957],
[ 2.84521151, 0.08709242, 0.74417454],
[ 0.01912885, 2.59781313, 3.72367549]], dtype=float32)]The second useful attribute is the updates attribute, used to set new values to shared variables once the expression has been evaluated:
>>> w = shared(1.0)
>>> x = T.scalar('x')
>>> mul = theano.function([x],updates=[(w,w*x)])
>>> mul(4)
[]
>>> w.get_value()
array(4.0)Such a mechanism can be used as an internal state. The shared variable w has been defined outside the function.
With the givens parameter, it is possible to change the value of any symbolic variable in the graph, without changing the graph. The new value will then be used by all the other expressions that were pointing to it.
The last and most important feature in Theano is the automatic differentiation, which means that Theano computes the derivatives of all previous tensor operators. Such a differentiation is performed via the theano.grad operator:
>>> a = T.scalar() >>> pow = a ** 2 >>> g = theano.grad(pow,a) >>> theano.printing.pydotprint(g) >>> theano.printing.pydotprint(theano.function([a],g))
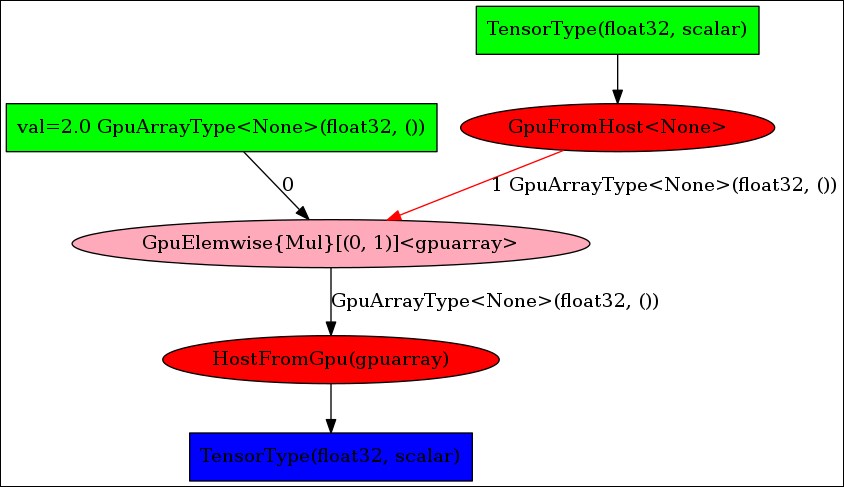
In the optimization graph, theano.grad has computed the gradient of  with respect to
with respect to a, which is a symbolic expression equivalent to 2 * a.
Note that it is only possible to take the gradient of a scalar, but the wrt variables can be arbitrary tensors.


























































