Finding prime factors
Prime factors (http://en.wikipedia.org/wiki/Prime_factor) are prime numbers that divide an integer exactly without a remainder. Finding prime factors seems almost impossible to crack. However, using the right algorithm—Fermat's factorization method (http://en.wikipedia.org/wiki/Fermat%27s_factorization_method) and NumPy—it becomes very easy. The idea is to factor a number N into two numbers c and d, according to the following equation:
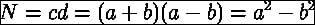
We can apply the factorization recursively, until we get the required prime factors.
How to do it...
The algorithm requires us to try a number of trial values for a.
Create an array of trial values.
It makes sense to create a NumPy array and eliminate the need for loops. However, you should be careful to not create an array that is too big in terms of memory requirements. On my system, an array of a million elements seems to be just the right size:
a = numpy.ceil(numpy.sqrt(n)) lim = min(n, LIM) a = numpy.arange(a, a + lim) b2 = a ** 2 - n
We...
































































