A primer on correlation and covariance structures
In the case of both PCA and FA, it is worth taking a moment to review some basic mathematical properties of covariances and correlations. Covariance is a measure of the linear codependence of two variables. Correlation is the covariance divided by the product of the standard deviation of the two variables. Thus, the correlation is a scaled covariance. In this chapter, we will be placing these covariances or correlations into matrices, called covariance matrices or correlation matrices.
The correlation matrix is a square matrix that has as many rows (and as many columns) as there are variables. Each element of the matrix represents the correlation between two variables. For example, in a dataset with three variables, A, B, and C, the correlation matrix would be as follows:
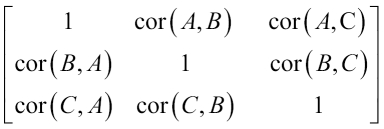
The diagonals are all 1 because the correlation of a variable with itself is 1. In a covariance matrix, the variances of the variables fall along the diagonal.























































