What if the data cannot be optimally partitioned using a linear decision boundary? In such a case, we say the data is not linearly separable.
The basic idea to deal with data that is not linearly separable is to create nonlinear combinations of the original features. This is the same as saying we want to project our data to a higher-dimensional space (for example, from 2D to 3D) in which the data suddenly becomes linearly separable. This concept is illustrated in the following figure:
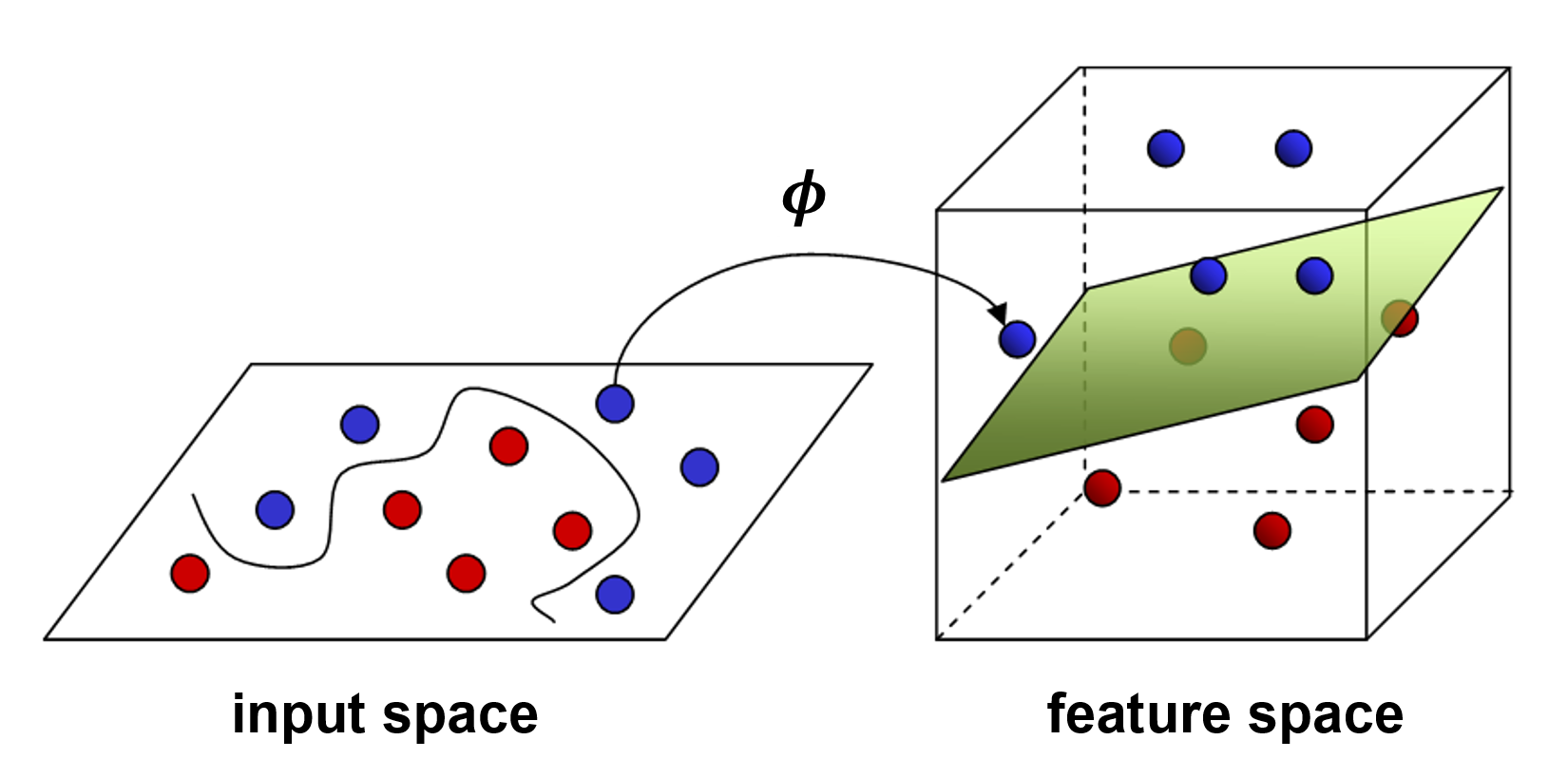
If data in its original input space (left) cannot be linearly separated, we can apply a mapping function ϕ(.) that projects the data from 2D into a 3D plane. In this higher-dimensional space, we may find that there is now a linear decision boundary (which, in 3D, is a plane) that can separate...



























































