Self-balancing trees
Now that you have learned how to work with BST, you can dive into the study of trees if you want to.
BST has a problem: depending on how many nodes you add, one of the edges of the tree can be very deep, meaning a branch of the tree can have a high level and another branch can have a low level, as shown in the following diagram:
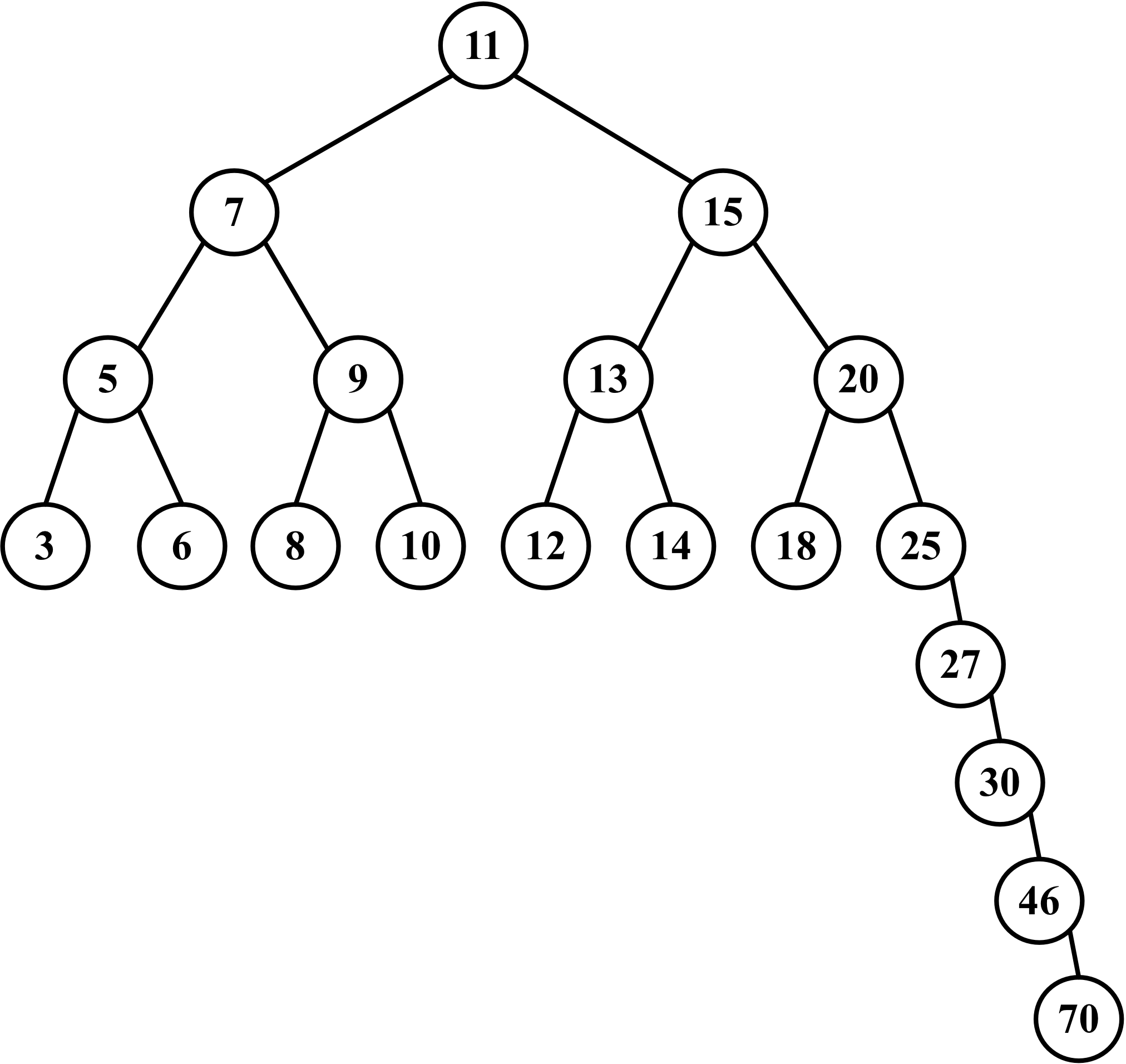
This can cause performance issues when adding, removing, and searching for a node on a particular edge of the tree. For this reason, there is a tree called the Adelson-Velskii and Landi's tree (AVL tree). The AVL tree is a self-balancing BST, which means the height of both the left and right subtrees of any node differ by 1 at most. You will learn more about the AVL tree in the following topic.
Adelson-Velskii and Landi’s tree (AVL tree)
The AVL tree is a self-balancing tree, meaning the tree tries to self-balance whenever a node is added to it or removed from it. The height of the left or right subtree of any node (and any level) differs by 1 at...

































































