7.2 Bras and kets
It’s now time to formalize our understanding of |0⟩ and |1⟩ and relate them to the discussion of linear algebra in Chapter 5, “Dimensions.”
When we previously looked at vector notation in section 5.4.2, we saw several forms, such as bra ket vector$bra vector$ket Dirac, Paul Dirac bra-ket notation ⟨ | (bra) | ⟩ (ket)

We now add two more invented by Paul Dirac, an English theoretical physicist, for use in quantum mechanics. They simplify many of the expressions we use in quantum computing.
Given a vector v = (v1, v2, …, vn), we denote by ⟨v|, pronounced “bra-v,” the row vector
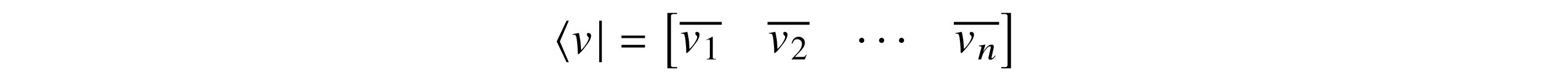
where we take the complex conjugate of each entry.
For w = (w1, w2, …, wm), |w⟩, pronounced “ket-w,” is the column vector
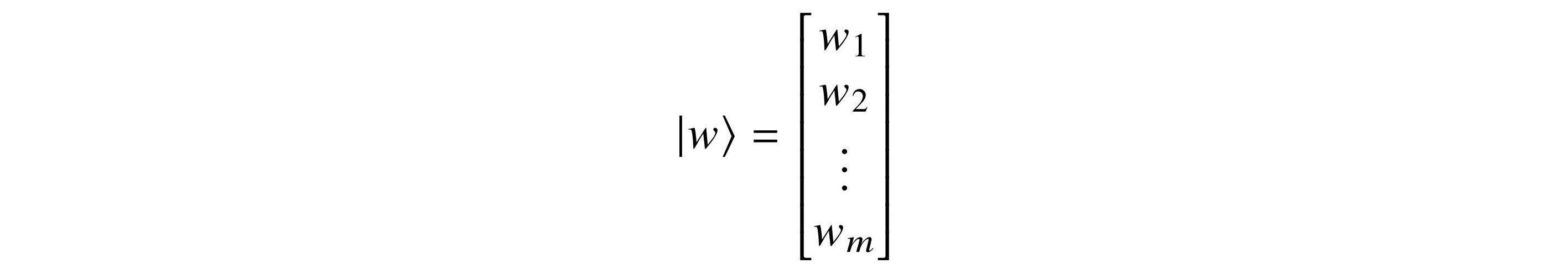
without the conjugations.
To avoid notational overload, I continue to put vector...































































