Introduction

Graphs enable solving certain data problems more easily and intuitively. At the core of a graph lies concepts of edges, nodes (or vertices), and their properties. For example, the following are two seemingly disconnected graphs. The left one represents a social network and the relationship (the edges of the graph) between friends (the vertices of the graph), while the right one is a graph that represents restaurant recommendations. Note that the vertices for our restaurant recommendations are not only the restaurants themselves but also the cuisine type (for example, Ramen) and location (for example, Vancouver, B.C., Canada); these are the properties of the vertices. This ability to assign nodes to virtually anything and use edges to define the relationship between these nodes is the greatest virtue of graphs, that is, their flexibility:

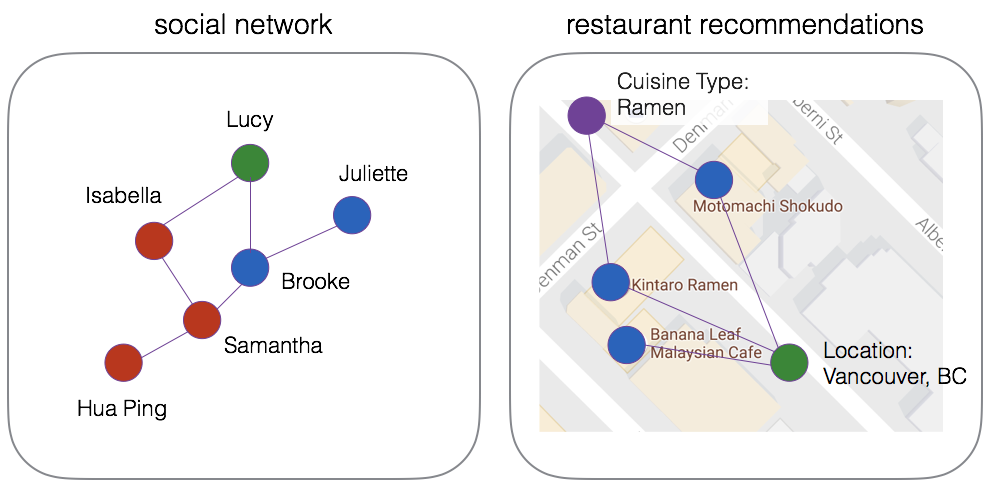
This flexibility allows us to conceptually connect these two seemingly disparate graphs into one common graph. In this case, we can join the...