Angles
We have had a brief introduction to the angle between vectors when we discussed the dot product and the magnitude of a vector. In this recipe, we will discuss how to find the actual angle between two vectors. The formula to find angle theta between two vectors is:
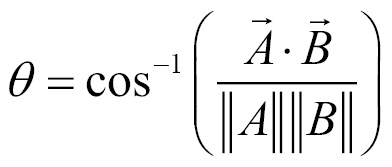
Getting ready
We have already implemented both the dot product and magnitude functions for vectors; this means we have everything needed to find the angle between two vectors already written. In general, this is a very expensive function, as it performs two square roots and an inverse cosine. Because it's such an expensive function, we try to avoid it whenever possible.
We can save a little bit of performance if, instead of multiplying the length of both vectors, we multiply the squared length of the vectors and then do just one square root operation on the result.
How to do it…
- Add the declaration of the angle function to
vectors.h:float Angle(const vec2& l, const vec2& r); float Angle(const vec3& l, const vec3& r);
- Provide the implementation of the angle function in
vectors.cpp:float Angle(const vec2& l, const vec2& r) { float m = sqrtf(MagnitudeSq(l) * MagnitudeSq(r)); return acos(Dot(l, r) / m); } float Angle(const vec3& l, const vec3& r) { float m = sqrtf(MagnitudeSq(l) * MagnitudeSq(r)); return acos(Dot(l, r) / m); }
How it works…
This formula relies on the geometric definition of the dot product:

This formula states that the dot product of two vectors is the cosine of the angle between them multiplied by both of their lengths. We can rewrite this formula with the cosine being isolated if we divide both sides by the product of the lengths of  and
and  :
:
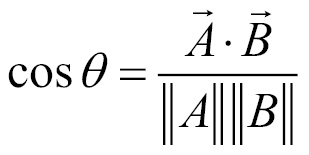
We can now use the inverse of cosine, the arc cosine (acos), to find the angle theta:
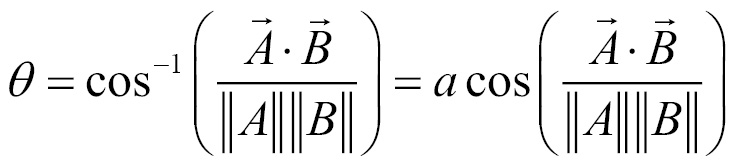
There's more…
The acos function we used to find the angle between vectors comes from the standard C math library. This implementation of acos returns radians, not degrees. It's much more intuitive to think of angles in terms of degrees than radians.
Radians and degrees
Add the following macros to the top of the vectors.h header file:
#define RAD2DEG(x) ((x) * 57.295754f) #define DEG2RAD(x) ((x) * 0.0174533f)
Using these macros you can convert between radians and degrees. For example, if you wanted to get the angle in degrees between vectors  and
and  , you could use the following code:
, you could use the following code:
float degrees = RAD2DEG(Angle(A, B));
If you are interested in the math used to derive these numbers, I suggest watching the following Khan Academy video:


























































