Estimating with support vector regression
As the name implies, SVR is part of the support vector family and a sibling of the Support Vector Machine (SVM) for classification (or we can just call it SVC).
To recap, SVC seeks an optimal hyperplane that best segregates observations from different classes. In SVR, our goal is to find a decision hyperplane (defined by a slope vector w and intercept b) so that two hyperplanes 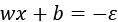 (negative hyperplane) and
(negative hyperplane) and  (positive hyperplane) can cover the
(positive hyperplane) can cover the  bands of the optimal hyperplane. Simultaneously, the optimal hyperplane is as flat as possible, which means w is as small as possible, as shown in the following diagram:
bands of the optimal hyperplane. Simultaneously, the optimal hyperplane is as flat as possible, which means w is as small as possible, as shown in the following diagram:
Figure 9.13: Finding the decision hyperplane in SVR
This translates into deriving the optimal w and b by solving the following optimization problem:
- Minimizing

- Subject to
 , given a training set of
, given a training set of  ,
,  , …
, …  …,
…, 
The theory behind SVR is very similar to SVM. In the next section, let...
































































