Calculating the distance
How do we calculate a distance? Well, that depends on the kind of problem. In two-dimensional space, we used to calculate the distance between two points, (x1, y1) and (x2, y2), as
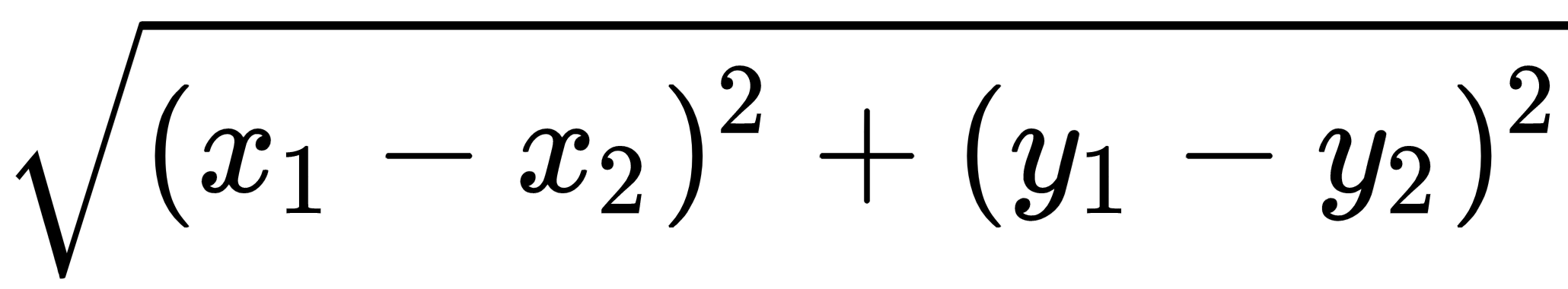
—the Euclidean distance. But this is not how taxi drivers calculate distance because in the city you can't cut corners and go straight to your goal. So, they use (knowing it or not) another distance metric: Manhattan distance or taxicab distance, also known as l1-norm:
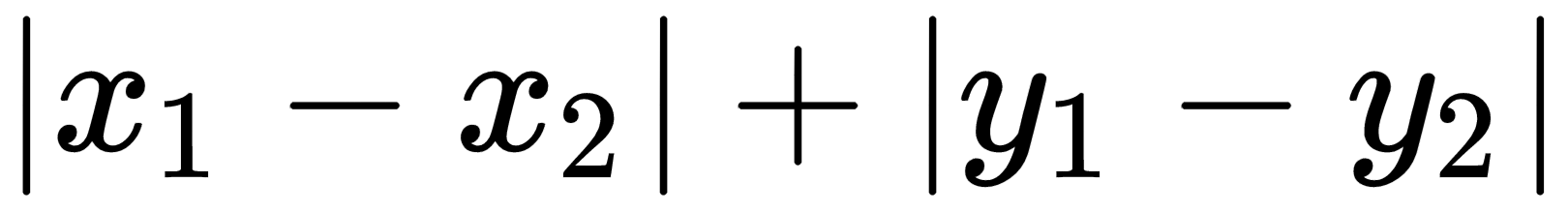
. This is the distance if we're only allowed to move along coordinate axes:
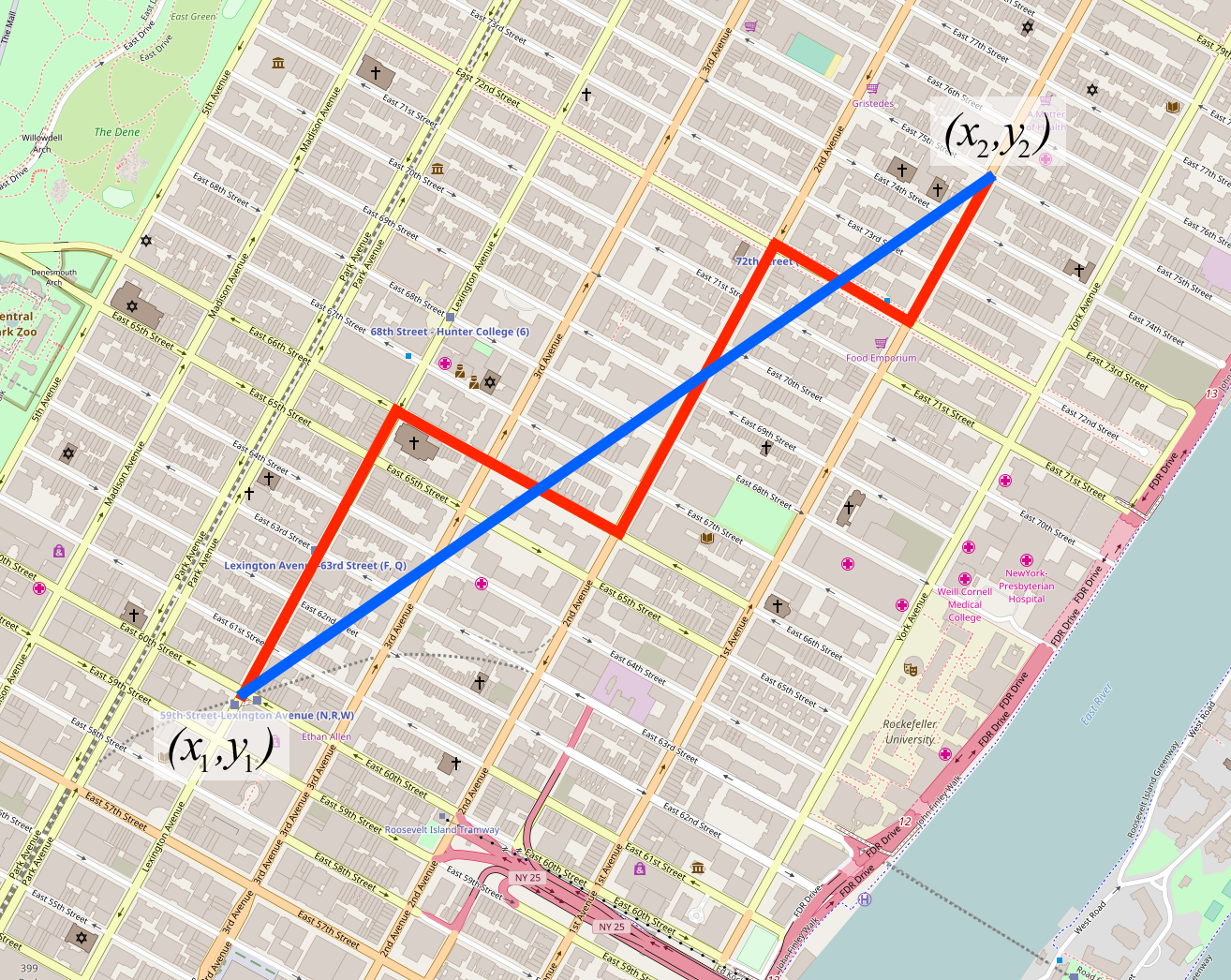
Figure 3.1: The blue line represents the Euclidean distance, the red line represents the Manhattan distance. Map of Manhattan by OpenStreetMap
Jewish German mathematician Hermann Minkowski proposed a generalization of both Euclidean and Manhattan distances. Here is the formula for the Minkowski distance:
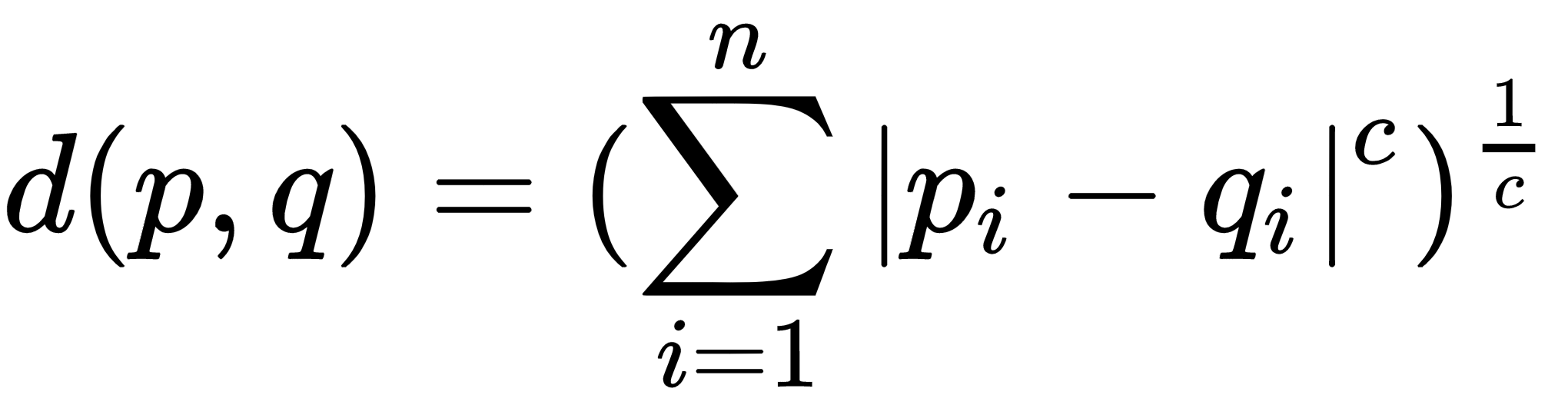
where p and q are n-dimensional vectors (or coordinates of points in n-dimensional space if you wish). But what does c stand for? It is an order of...





























































