Understanding the wallet technology

An Ethereum wallet is a digital tool designed to store, manage, and interact with Ethereum. This wallet acts as a secure gateway, allowing users to send, receive, and store Ether, as well as interact with various Decentralized Applications (DApps) built on the Ethereum network. Ethereum wallets come in different forms, including software-based wallets, hardware wallets, and web-based wallets, each offering its own set of features, accessibility, and security measures. These wallets generate unique addresses for users, serving as their digital identity on the Ethereum network. With an Ethereum wallet, individuals can participate in the exciting world of Decentralized Finance (DeFi), trade cryptocurrencies, and engage in smart contract interactions, all while maintaining control over their private keys and ensuring the safety of their digital assets.

Ethereum wallets can also come in the form of non-deterministic wallets or deterministic wallets. We will learn more about what non-deterministic or deterministic wallets are in the next section.

Understanding non-deterministic and deterministic wallets

What’s the difference between these two types of wallets? They are different in how the private keys are backed up. A non-deterministic wallet generates private keys that are random and independent of each other (as on the left-hand side of the following diagram). There is no particular pattern as to how the keys are derived; hence, we need to create a backup of the key every time a new one is generated. In a deterministic wallet, on the contrary, the private keys are related because they originate from the same key called a seed, as shown here on the right-hand side of the diagram. Just backing up the seed once will be enough to regenerate all the keys:

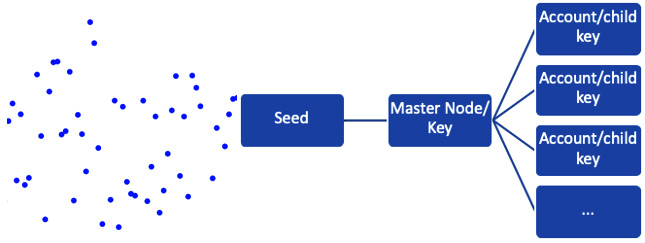
Figure 14.1 – Non-deterministic wallet and deterministic wallet

There are three types of wallets:

• Deterministic wallet
• HD wallet
• Armory deterministic wallet

The first wallet, which is used in an Ethereum presale, is a non-deterministic wallet. It’s considered a rather old style compared to a deterministic wallet. Modern deterministic wallets have advantages over non-deterministic wallets in many aspects, such as backups, security, data storage, accounting, auditing, and access controls. The following list showcases some of these advantages:

• A one-time backup for deterministic wallets is so much easier than the cumbersome way a non-deterministic wallet has to be backed up. If you don’t create a backup every time, you will risk losing the data that refers to ether and smart contracts. For a deterministic wallet, only copying the master seed will be enough. It’s less work during the import and export of wallets. For a non-deterministic wallet, the entire list of keys needs to be copied during the migration process.
• With the concept of deterministic wallets, deriving the keys from the seed makes it possible to store the private keys offline. Disabling web server access to private keys offers more privacy and security. Securing the seed takes less effort compared to keeping all the keys safe, which is what non-deterministic wallets need to do.

The HD wallet is the most well-known kind of deterministic wallet. It’s also a preferred option among the deterministic wallets if you want to create one since it is well developed. When it comes to the following cases, the HD wallet shows more advantages than other types of deterministic wallets:

• Use cases for creating public keys without accessing the corresponding private keys
• Use cases for keys matching the hierarchical structure in an organizational context

The first use case shows the security advantage of the HD wallet. Normally, a deterministic wallet holds a single chain of keypairs, which doesn’t support selective keypair sharing, while the HD wallet allows such selective sharing for multiple keypair chains that are generated from a single root. In some cases, being able to create public keys without exposing private keys makes the HD wallet available in environments that would normally be a higher security risk. The second use case listed here takes advantage of the hierarchical structure of the design and applies it to real-world cases.

An HD wallet has the security advantages just mentioned previously, but we will bring up another aspect of secure consideration—private key management. It not only refers to key generation offline (away from the network, such as cold storage). Key sharding and splitting or division of signatures are other alternatives. Key sharding, also known as Shamir’s secret sharing, is basically splitting a key into several pieces, or shards. This makes each shard useless, and the original key will be reconstructed unless enough pieces are assembled to reconstruct it. A similar but very different concept to this is a multi-signature wallet. Readers who are interested in the topic are encouraged to do further reading about this.

With cryptocurrency wallets becoming more and more developed, protocols and standards need to be shared across the industry. The Ethereum community has been establishing standards over the years. Some of them are known as Ethereum Improvement Proposals (EIPs). Some are application-level standards, for example, the standard format for smart contracts, known as Ethereum Requests for Comment (ERC). Standards are also followed for wallet creation. There are a few standards that are widely adopted, as follows:

• HD wallets (BIP-32)
• Multipurpose HD wallets (BIP-43)
• Multi-currency and multi-account wallets (BIP-44)
• Mnemonic code words (BIP-39)

BIP stands for Bitcoin Improvement Proposal. Although there are so many differences between the Bitcoin and Ethereum networks today, they still have a lot in common and share standards and protocols.

The mnemonic code word is 128-bit to 256-bit entropy. This entropy will be plugged into a Password-Based Key Derivation Function 2 (PBKDF2) function and stretched into a 512-bit seed. The seed will be used in building a deterministic wallet. We will take a look at those standards in detail next.

Mnemonic code words (BIP-39)

The purpose of BIP-39 is to implement mnemonic code for generating deterministic keys. The standard defines two processes:

• Generating the mnemonic words
• Converting the words into binary seeds

The guideline of BIP-39 is basically transforming the randomness generated in computer language into human language. The transformation starts with entropy and ends with a mapped mnemonic sentence, with a middle product checksum. The transformation can be simplified to the following:

Entropy >>> Checksum >>> Entropy + checksum >>> Mnemonic sentence

The initial entropy size is defined as 128 to 256 bits. As entropy becomes more secure, the end product sentence gets longer. If we take a 128-bit entropy, we will get 12 phrases. We summarize the size of the value of each step in bits, as shown in the following table:

Entropy	Checksum	Entropy + checksum	Mnemonic sentence
128	4	132	12
160	5	165	15
192	6	198	18
224	7	231	21
256	8	264	24

Table 14.1 – Entropy sizes

The generation process of mnemonic words can be broken down into the following steps:

1. Generate an initial entropy, that is, a cryptographically random sequence.

For example, we have entropy in hexadecimal, like so:

7f7f7f7f7f7f7f7f7f7f7f7f7f7f7f7f

2. Generate a checksum of entropy by taking the first n bits of entropy’s SHA-256 hash.

n =  length of entropy  ____________ 32 

We won’t go into the details of the SHA-256 algorithm here. You can directly take the SHA-256 hash of entropy from an online tool such as https://emn178.github.io/online-tools/sha256.html. The hash we get is similar to the following in hexadecimal:

8ecee7af753ae153af3163ac2a5d7a73381bfb1dff5f45a06f4e2d673b4ee41c

Convert the hash from hexadecimal into binary, as follows:

10001110110 01110111001 11101011110 11101010011 10101110000 10101001110 10111100110 00101100011 10101100001 01010010111 01011110100 11100110011 10000001101 11111101100 01110111111 11101011111 01000101101 00000011011 11010011100 01011010110 01110011101 10100111011 10010000011 100

The next step is to get n, which we do by applying the equation we mentioned previously to the 128-bit entropy we had:

n =  128 _ 32  = 4

Therefore, n is 4; we are taking the first 4 bits of the hash. It will be 1,000 in our case.

3. Append the checksum to the end of the entropy. The raw binary of the original entropy will be like the following:

01111111011 11111011111 11011111110 11111110111 11110111111
           10111111101 11111101111 11101111111 01111111011 11111011111
           11011111110 1111111

Append 1000 to the end of the 128-bit binary. We will get a total of 132 bits (128 + 4 bits):

           01111111011 11111011111 11011111110 11111110111 11110111111
           10111111101 11111101111 11101111111 01111111011 11111011111
           11011111110 11111111000

4. Convert the 132-bit binary into decimal, like so:

           01111111011 11111011111 11011111110 11111110111 11110111111
           1019              2015             1790             2039             1983
           10111111101 11111101111 11101111111 01111111011 11111011111
           1533              2031             1919             1019             2015
           11011111110 11111111000
            1790             2040

5. Match the word indexes with a word list. We will get the following 12 phrases:

1019, 2015, 1790, 2039, 1983, 1533, 2031, 1919, 1019, 2015, 1790,  2040

Our resulting 12 phrases are as follows:

• Let’s use the English list (https://github.com/bitcoin/bips/blob/master/bip-0039/english.txt):

  legal winner thank year wave sausage worth useful legal winner thank yellow

• Then, let’s try the Japanese list (https://github.com/bip32JP/bip32JP.github.io/blob/master/test_JP_BIP39.json):

  そつう れきだい ほんやく わかす りくつ ばいか ろせん やちん そつう れきだい ほんやく わかめ

Please try this transformation process on your own and get familiar with the process.

Stretching mnemonic code words into the seed of the deterministic wallet

Now that we’ve learned step by step how mnemonic code words are generated, we will go into more detail about how the mnemonic code words are transformed into a seed, which will be used in deterministic wallet creation. The process can be broken down into a few steps:

1. Take the mnemonic code words as a parameter for the PBKDF2 function. We will use the Japanese words from the previous section:

   そつう れきだい ほんやく わかす りくつ ばいか ろせん やちん そつう れきだい ほんやく わかめ

2. Take the salt as another parameter for the PBKDF2 function. The salt, known as a cryptographic salt, is a string. It has two components—a constant mnemonic string and a passphrase provided by the user. The passphrase is generally optional. The purpose of introducing the salt is to make the end product seem more secure.

For example, we use the following Japanese phrase as a passphrase:

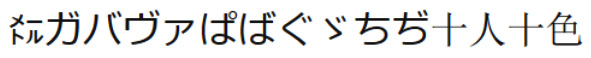
Figure 14.2 – Japanese passphrase

3. Use the PBKDF2 function to get a 512-bit mnemonic seed, with the parameters from the previous two steps as inputs. What a PBKDF2 function does is basically apply a pseudorandom function—in this case, a Hash-based Message Authentication Code (HMAC), to the inputs.

The PBKDF2 key derivation function can be described with the following formula:

Seed = PBKDF2(PRF, Password, Salt, c, dkLen)

The parameters are explained as the following:

• RPF: The pseudorandom function HMACSHA512
• c: The number of iterations, which in this case is 2048
• dkLen: The desired bit-length of seed, which is 512

With the transformation complete, we got our seed:

aee025cbe6ca256862f889e48110a6a382365142f7d16f2b9545285b3af64e542143a577e9c144e101a6bdca18f8d97ec3366ebf5b088b1c1af9bc31346e60d9

The following are a few implementations in different languages for reference:

Language	Library Path
C	https://github.com/ElementsProject/libwally-core
C ++	https://github.com/libbitcoin/libbitcoin-system
Go	https://github.com/tyler-smith/go-bip39go-bip39
JavaScript	https://github.com/bitcoinjs/bip39
Python	https://github.com/trezor/python-mnemonic
Ruby	https://github.com/lian/bitcoin-ruby/blob/master/lib/bitcoin/trezor/mnemonic.rb
Rust	https://github.com/infincia/bip39-rs
Swift	https://github.com/CikeQiu/CKMnemonic https://github.com/yuzushioh/HDWalletKit

Table 14.2 – Library paths

More information can be found on the wiki page here: https://github.com/bitcoin/bips/blob/master/bip-0039.mediawiki. You are welcome to read through for more details.

HD wallets (BIP-32)

HD wallets follow the BIP-32 standard, which was created on February 11, 2012. The standard was set for mainly two aspects:

• How to use a single seed to derive a tree of keypairs
• How to derive wallet structure from a tree of keypairs

Deriving a tree of keypairs

Before going into any details regarding key derivation, we need to understand the concept of extended keys properly. The concept of extended keys came into the picture to prevent the derived child keys from entirely depending on the parent key itself. The process for deriving the child keys is as follows:

1. Take the private and public parent key.
2. Extend the key with an extra 256-bit entropy, called a chain code:
   1. If the parent key is a private key, the extended private key will be prefixed with xprv
   2. If the parent key is a public key, the extended public key will be prefixed with xpub
3. The extended keys will be used to produce the child key instead of the original private and public parent keys.

For key derivation, Child Key Derivation (CKD) functions are defined. They are functions that are used to derive child keys from a parent key. There will be a different CKD for each computation of the following:

• Computing the private child key from the private parent key
• Computing the public child key from the public parent key
• Computing the public child key from the private parent key

The parent key doesn’t need to be the root of the tree, and it can be any node on the tree. To summarize, there are two ways to generate a child public key:

• Directly from the parent public key
• From the child private key

Notice it won’t be possible to compute a private child key from a public parent key.

However, the feature of generating child public keys from parent public keys only is a key feature of the HD wallet. This brings us back to the second point of advantage deterministic wallets have over non-deterministic ones (which we went over in the Understanding non-deterministic and deterministic wallets section). With an extended public key on a web server, we can generate as many public keys and addresses as we need. If it wasn’t an HD wallet, we would have to store all those public keys and addresses on a server, which is more work for maintenance and security. On the other hand, extended private keys can be secured on a separate server or in an offline cold wallet. Even if the server holding the public keys is compromised, the private keys won’t be impacted.

Like a coin with two faces, the convenience of generating all the public child keys from the extended public key also comes with risks. Recall the process of generating extended keys. In the second step, we extend the public key with a chain code. If the attacker gets the chain code from the extended public key, it will compromise the non-hardened child key. With the child private key plus the chain code, the attacker will be able to derive the parent private key. Other than extended keys, we will introduce another concept, that is, hardened and normal (unhardened or non-hardened) keys. Here, we simplify the computation of those keys as follows:

• Hardened child key: Hash (parent private key + index)
• Normal child key: Hash (parent public key + index)

For the hardened child key, the linkage between the parent public key and private child key is broken. Therefore, the risk of exposing the child and parent private keys is countered.

In the formula for hardened and normal child keys, we are using an index. To generate more than one child key from a certain parent key, an index is very useful for keeping things in order. The index is defined as a 32-bit integer. Just like how we distinguish private and public extended keys using the xprv and xpub prefixes, we use different ranges of indexes for hardened and normal child keys:

• The index of a hardened child key is in the range [0,2 31] or [0, 2 31 - 1]
• The index of a normal child key is bigger than 2 31 - 1

With all the concepts of keys in mind, let’s move on to the key derivation process. Instead of solely using one key, both private and public keys are used in an extension with an extra 256 bits of entropy. With all CKDs in place, the key tree can be built. Building the key tree takes on the following process:

1. First, we start with one master extended key.
2. Then, we use the CKD function to get level-one derived nodes.
3. Next, we apply CKD functions to each of these level-one nodes to derive next-level nodes.
4. Finally, we repeat the same process to build the entire tree.

The keys are in the format of 256 bits, while there are 2 256 possible extended keypairs in total. Because of security considerations, master keys won’t be generated, but are generated from seed values instead.

Deriving the wallet structure

Having a tree of key pairs, the structure of a wallet can be imposed on the tree. The default wallet layout is defined like so:

• Each account contains one external and one internal keypair chain
• Public addresses are derived from external keychains
• The internal keychain is responsible for all the activities that won’t be shared with the outside environment

HD wallets support a lot of use cases, for example, the following:

• Full wallet sharing
• Support for auditing
• Central control from headquarters to branches
• Recurrent transactions among businesses
• Separating incoming and outgoing transactions to prevent fraud

When it’s for accounting and auditing purposes, accountants or auditors need to read the history of transactions. For accessing these transactions, wallet owners can generate the public keys at the hierarchical level needed. In terms of access control, the owner of the HD wallet will have the flexibility to determine how much ether others can spend by designing the hierarchy of the wallet.

For implementations, there are quite a few packages in different languages. We are only listing a few here for reference:

Language	Library
C ++	mSIGNA: https://github.com/ciphrex/mSIGNA
Go	btcutil: https://github.com/btcsuite/btcutil go-hdwallet: https://github.com/wemeetagain/go-hdwallet
Java	supernode: https://github.com/bitsofproof/supernode bushido-java-core: https://github.com/bushidowallet/
Python	pycoin: https://github.com/richardkiss/pycoin bip32utils 0.3.post4: https://pypi.org/project/bip32utils/
Ruby	money-tree: https://github.com/GemHQ/money-tree

Table 14.3 – Wallet implementations

You can extend your reading to the wiki page of this standard: https://github.com/bitcoin/bips/blob/master/bip-0032.mediawiki. More math and details are shared on this page.

HD wallet paths

If you have been doing extra reading on BIP 32, you will have noticed a picture of key derivation, which can be found here: https://github.com/bitcoin/bips/blob/master/bip-0032/derivation.png. In this picture, the master node at depth 0 has a notation of m. At depth 1, wallets have notations such as m/0, m/1, and so on. And for depth 2, wallets have notations such as m/0/0, m/0/1, ..., m/i/0, and m/i/1.

This is another convention for keys in HD wallets. All keys are formatted like a path. It’s defined as follows:

• The master private key is m.
• The first normal child of the master private key is m/0.
• The first hardened child of the master private key is m/0’. 4. The first normal child of m/0’ is m/0’/0 and so on.

The last number of the path describes which is the child of the parent, and the rest of the path is the parent. You may see keys such as M/1/0. That means it’s a public key. Public keys start with an uppercase M while private keys start with a lowercase m.

We know one parent extended key can have more than one child key and that the upper limit of the number of child keys is about 4 billion—2 billion of each hardened and normal child key. Therefore, the entire tree of HD wallets that is described in BIP-32 can end up being very deep and wide. To reduce the degrees of freedom that BIP-32 offers, BIP-43 and BIP-44 were introduced to further standardize the structure of the tree of HD wallets.

Multipurpose HD wallets (BIP-43)

BIP-43 uses the first level of the BIP-32 tree structure as purpose:

m / purpose' /*

From the purpose value, we can tell it’s the hardened child key that has been proposed. HD wallets that follow BIP-43 are only using branch m/ i’ /... for certain purposes. Index i is used to identify the purpose.

Multi-currency and multi-account wallets (BIP-44)

BIP-44 is actually a particular application of BIP-43. BIP-44 has the title multi-account hierarchy for deterministic wallets. It supports the following features:

• Multiple accounts
• Multiple coins
• External chains per account
• Internal chains per account
• Millions of addresses per chain

In BIP-44, five levels in the BIP-32 path are defined like so. Notice that the fourth and fifth levels are not hardened derivations like the previous three levels:

m / purpose' / coin_type' / account' / change / address_index

We will explain each level in detail:

1. The purpose is set to a constant 44’. Notice that a hardened child key is used.
2. The coin type varies, depending on the type of cryptocurrency. We’ve listed a few that interest us:

Coin type index	Coin
0’	Bitcoin
60’	Ether
61’	Ether Classic
1’	Testnet for all coins

Table 14.4 – Coin types

Please take some time to check the whole list: https://github.com/satoshilabs/slips/blob/master/slip-0044.md.

3. The account allows independent user identities. Also, different types of coins don’t mix together in different accounts.

4. change is used to identify external and internal chains:

• The external chain is set as constant 0
• The internal chain is set as constant 1

In the scope of Ethereum, only the external chain is used to receive the funds. The normal derivation, instead of the hardened derivation that’s used here, is used to support exporting the extended public keys to an environment that may not be secured.

5. The address index is a public derivation, the same as change.

Looking into the details of the standards of HD wallets, you should be able to understand any user-facing blockchain application better now.

Generating a private key in Ethereum

With a sound understanding of wallets, we will go into the details of private key generation in this section. The private key is a key concept in Ethereum. The address of externally owned accounts is determined by a private key. Each address and private key is used to derive that the address is unique. The private key is stored locally only, and won’t be shared in transactions. The address of the account and digital signature are shared instead. The creation of a digital signature needs the participation of a private key. The digital signature is then used in the authentication that’s needed by transactions.

The journey from a private key to an address is as follows:

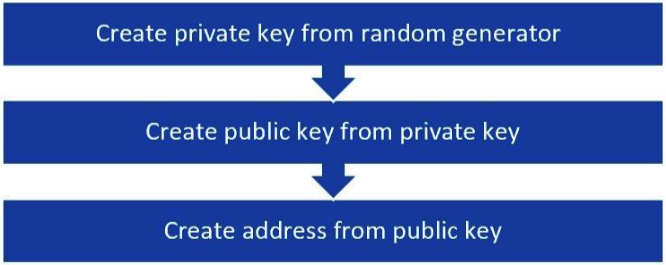
Figure 14.3 – Private key

The private key in Ethereum is defined as a random number with the format of 256 bits, 32 bytes, a 64-hexadecimal-digits HEX string, and any number between 1 and 2 256.

The generation of the private key is an offline activity. It’s important to use a true random number generator to generate the private key.

web3.utils provides a utility function to generate pseudo-random HEX strings given the byte size. The randomHex library uses crypto.randomBytes() in Node.js, as shown in the following code:

$ npm install web3
   web3.utils.randomHex(32)
 $ npm install randomhex
   var randomHex = require('randomhex');
   randomHex(32, console.log);

Once the private key is generated, the public key can be derived from a private key using the following formula for an elliptic curve:

Public key = Private Key * G

In the previous formula, the following applies:

• G refers to the generator point.
• The elliptic curve allows the multiplication operation, but it cannot perform the reverse operation: division.

In other words, the public key can be derived easily but it is not possible to use the public key to calculate another private key. The one-way nature of the elliptic curve suits our needs for security. This type of cryptography is known as asymmetric cryptography. There is more than one elliptic curve out there. Both Ethereum and Bitcoin use the elliptic curve known as secp256k1. There are a few libraries available for the secp256k1 elliptic curve:

• secp256k1: A library wraps the bitcoin secp256k1 C library
• The libsecp256k1 wrapper for OCaml: A library wraps the secp256k1 EC(DSA) library into an OCaml library

The following code will convert a private key into a public key:

   npm install elliptic-curve
   var secp256k1 = require('elliptic-curve').secp256k1
   var privateKey =
   '278a5de700e29faae8e40e366ec5012b5ec63d36ec77e8a2417154cc1d25383f'
   secp256k1.getPublicKey(privateKey)
   '03fdd57adec3d438ea237fe46b33ee1e016eda6b585c3e27ea66686c2ea5358479'

The previously installed package is a plain JavaScript implementation of elliptic-curve. Compared to RSA cryptography, the elliptic curve is slower, and the JavaScript implementation is even slower. The library is intended to be a fast implementation.

By using the format established by the Standard for Efficient Cryptography Group, the public key uses 65 bytes and 130 hexadecimal characters. Ethereum uses an uncompressed point on the elliptic curve with the prefix 0x04. The public key that’s derived from the private key is a pair (x, y). The final public key we saw from the library is the result of serialization by concatenating 04, x, and y, as shown in the following formula:

Public Key = 04 + x in 64 hex + y in 64

An Ethereum address is described as follows in the yellow paper—for a given private key, pr, the Ethereum address A(pr) (a 160-bit value) to which it corresponds is defined as the rightmost 160 bits of the Keccak hash of the corresponding ECDSA public key.

In other words, from a public key to an address, Ethereum implements Keccak-256 to calculate the hash of this public key and the rightmost 20 bytes is the Ethereum address. When the public key is used in the calculation, the leading 04 is left out.

We will learn more about multiparty signature wallets in the next section.