Point and line
To test if a point is on a line, or to get the point on a line closest to a test point, we first have to project the point onto the line. This projection will result in a floating point value, t. We use this new t value to find the distance of the point along the line segment using the distance(t) = start + t * (end - start)function. The start point of the line is at t = 0, the end point is at t = 1. We have to take two edge cases into account, when t is less than 0 or greater than 1:
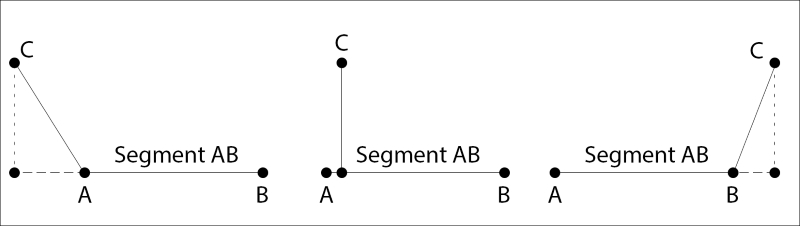
Getting ready
We are going to implement two functions, one to get the point on a line closest to a test point and one to determine if a test point is on a line. The ClosestPoint function is going to project the test point onto the line and evaluate the parametric function, distance(t) = start + t * (end - start).
To determine if a test point is on a line segment, we still need the point on the segment closest to the test point. We are then able to measure the distance between the test point and...




























































