Simply speaking, ensemble machine learning refers to a technique that integrates output from multiple learners and is applied to a dataset to make a prediction. These multiple learners are usually referred to as base learners. When multiple base models are used to extract predictions that are combined into one single prediction, that prediction is likely to provide better accuracy than individual base learners.
Ensemble models are known for providing an advantage over single models in terms of performance. They can be applied to both regression and classification problems. You can either decide to build ensemble models with algorithms from the same family or opt to pick them from different families. If multiple models are built on the same dataset using neural networks only, then that ensemble would be called a homogeneous ensemble model. If multiple models are built using different algorithms, such as support vector machines (SVMs), neural networks, and random forests, then the ensemble model would be called a heterogeneous ensemble model.
The construction of an ensemble model requires two steps:
- Base learners are learners that are designed and fit on training data
- The base learners are combined to form a single prediction model by using specific ensembling techniques such as max-voting, averaging, and weighted averaging
The following diagram shows the structure of the ensemble model:
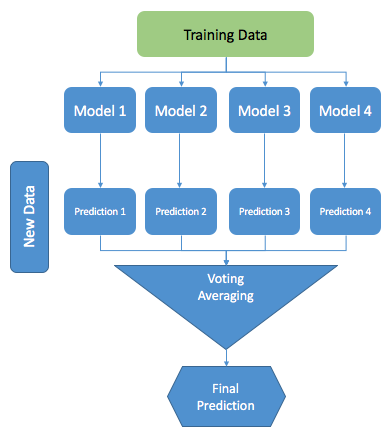
However, to get an ensemble model that performs well, the base learners themselves should be as accurate as possible. A common way to measure the performance of a model is to evaluate its generalization error. A generalization error is a term to measure how accurately a model is able to make a prediction, based on a new dataset that the model hasn't seen.
To perform well, the ensemble models require a sufficient amount of data. Ensemble techniques prove to be more useful when you have large and non-linear datasets.
Irrespective of how well you fine-tune your models, there's always the risk of high bias or high variance. Even the best model can fail if the bias and variance aren't taken into account while training the model. Both bias and variance represent a kind of error in the predictions. In fact, the total error is comprised of bias-related error, variance-related error, and unavoidable noise-related error (or irreducible error). The noise-related error is mainly due to noise in the training data and can't be removed. However, the errors due to bias and variance can be reduced.
The total error can be expressed as follows:
Total Error = Bias ^ 2 + Variance + Irreducible Error
A measure such as mean square error (MSE) captures all of these errors for a continuous target variable and can be represented as follows:
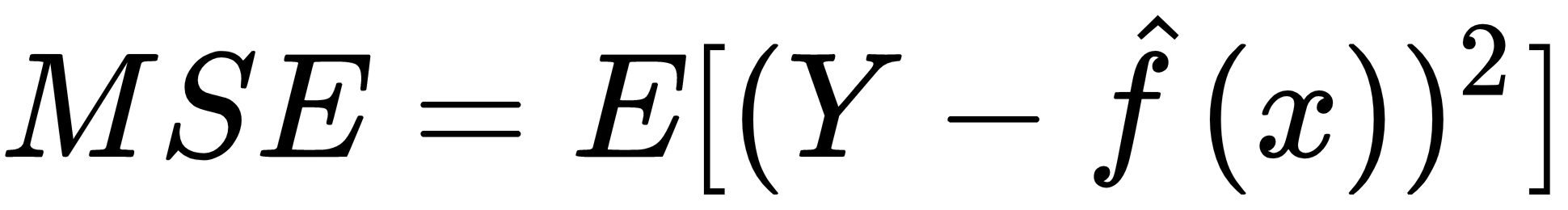
In this formula, E stands for the expected mean, Y represents the actual target values and 
is the predicted values for the target variable. It can be broken down into its components such as bias, variance and noise as shown in the following formula:
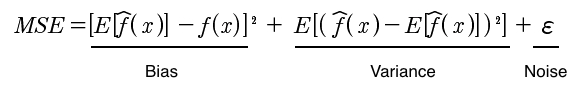
While bias refers to how close is the ground truth to the expected value of our estimate, the variance, on the other hand, measures the deviation from the expected estimator value. Estimators with small MSE is what is desirable. In order to minimize the MSE error, we would like to be centered (0-bias) at ground truth and have a low deviation (low variance) from the ground truth (correct) value. In other words, we'd like to be confident (low variance, low uncertainty, more peaked distribution) about the value of our estimate. High bias degrades the performance of the algorithm on the training dataset and leads to underfitting. High variance, on the other hand, is characterized by low training errors and high validation errors. Having high variance reduces the performance of the learners on unseen data, leading to overfitting.
