Building a smart temperature controller for your room
To control your room's temperature, we can build a smart temperature controller. In this case, we use a PID (proportional–integral–derivative) controller. When you set a certain temperature, a PID controller will change the temperature by turning either cooler or hotter. A PID controller program is developed using Python, which runs on the Raspberry Pi board.
Assume cooler and heater machines are connected via a relay. We can activate cooler and heater machine by sending HIGH signal on a relay.
Let's build!
Introducing PID controller
PID control is the most common control algorithm widely used in industry, and has been universally accepted in industrial control. The basic idea behind a PID controller is to read a sensor, then compute the desired actuator output by calculating proportional, integral, and derivative responses and summing those three components to compute the output.
An example design of a general PID controller is depicted in the following figure:
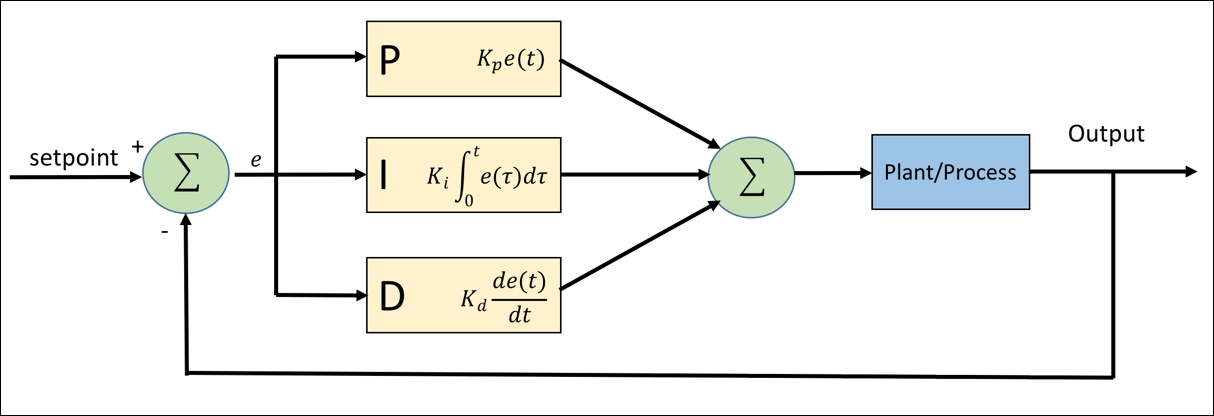
Furthermore, a PID controller formula can be defined as follows:
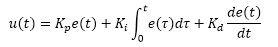
Kp, Ki , Kd represent the coefficients for the proportional, integral, and derivative. These parameters are non-negative values. The variable e represents the tracking error, the difference between the desired input value i, and the actual output y. This error signal e will be sent to the PID controller.
Implementing PID controller in Python
In this section, we will build a Python application to implement the PID controller. In general, our program flowchart can be described by the following figure:
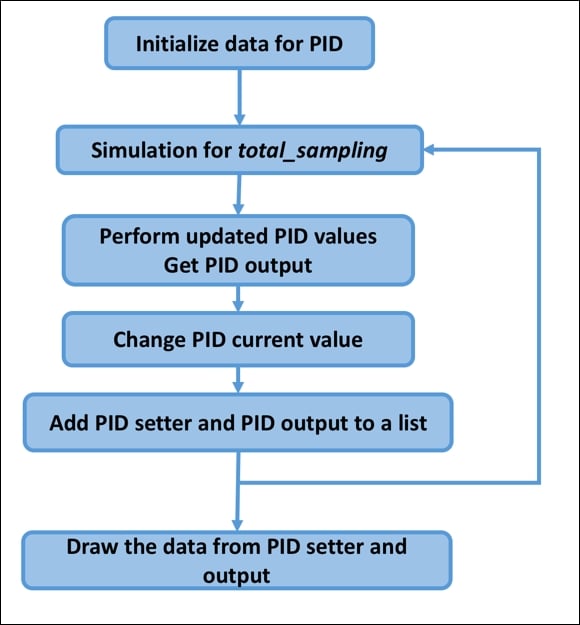
We should not build a PID library from scratch. You can translate PID controller formula into Python code easily. For implementation, I use the PID class from https://github.com/ivmech/ivPID. The following is the content of the PID.py file:
import time
class PID:
"""PID Controller
"""
def __init__(self, P=0.2, I=0.0, D=0.0):
self.Kp = P
self.Ki = I
self.Kd = D
self.sample_time = 0.00
self.current_time = time.time()
self.last_time = self.current_time
self.clear()
def clear(self):
"""Clears PID computations and coefficients"""
self.SetPoint = 0.0
self.PTerm = 0.0
self.ITerm = 0.0
self.DTerm = 0.0
self.last_error = 0.0
# Windup Guard
self.int_error = 0.0
self.windup_guard = 20.0
self.output = 0.0
def update(self, feedback_value):
"""Calculates PID value for given reference feedback
.. math::
u(t) = K_p e(t) + K_i \int_{0}^{t} e(t)dt + K_d {de}/{dt}
.. figure:: images/pid_1.png
:align: center
Test PID with Kp=1.2, Ki=1, Kd=0.001 (test_pid.py)
"""
error = self.SetPoint - feedback_value
self.current_time = time.time()
delta_time = self.current_time - self.last_time
delta_error = error - self.last_error
if (delta_time >= self.sample_time):
self.PTerm = self.Kp * error
self.ITerm += error * delta_time
if (self.ITerm < -self.windup_guard):
self.ITerm = -self.windup_guard
elif (self.ITerm > self.windup_guard):
self.ITerm = self.windup_guard
self.DTerm = 0.0
if delta_time > 0:
self.DTerm = delta_error / delta_time
# Remember last time and last error for next calculation
self.last_time = self.current_time
self.last_error = error
self.output = self.PTerm + (self.Ki * self.ITerm) + (self.Kd * self.DTerm)
def setKp(self, proportional_gain):
"""Determines how aggressively the PID reacts to the current error with setting Proportional Gain"""
self.Kp = proportional_gain
def setKi(self, integral_gain):
"""Determines how aggressively the PID reacts to the current error with setting Integral Gain"""
self.Ki = integral_gain
def setKd(self, derivative_gain):
"""Determines how aggressively the PID reacts to the current error with setting Derivative Gain"""
self.Kd = derivative_gain
def setWindup(self, windup):
"""Integral windup, also known as integrator windup or reset windup,
refers to the situation in a PID feedback controller where
a large change in setpoint occurs (say a positive change)
and the integral terms accumulates a significant error
during the rise (windup), thus overshooting and continuing
to increase as this accumulated error is unwound
(offset by errors in the other direction).
The specific problem is the excess overshooting.
"""
self.windup_guard = windup
def setSampleTime(self, sample_time):
"""PID that should be updated at a regular interval.
Based on a pre-determined sampe time, the PID decides if it should compute or return immediately.
"""
self.sample_time = sample_timeFor testing purposes, we create a simple program for simulation. We need required libraries such as numpy, scipy, pandas, patsy, and matplotlib libraries. First, you should install python-dev for Python development. Type the following commands in your Raspberry Pi Terminal:
$ sudo apt-get update $ sudo apt-get install python-dev
When done, you can install numpy, scipy, pandas, and patsy libraries. Open your Raspberry Pi Terminal and type the following commands:
$ sudo apt-get install python-scipy $ pip install numpy scipy pandas patsy
The last step is to install the matplotlib library from source code. Type the following commands on your Raspberry Pi Terminal:
$ git clone https://github.com/matplotlib/matplotlib $ cd matplotlib $ python setup.py build $ sudo python setup.py install
Once the required libraries are installed, we can test our PID.py file. Type the following program:
import matplotlib
matplotlib.use('Agg')
import PID
import time
import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import spline
P = 1.4
I = 1
D = 0.001
pid = PID.PID(P, I, D)
pid.SetPoint = 0.0
pid.setSampleTime(0.01)
total_sampling = 100
feedback = 0
feedback_list = []
time_list = []
setpoint_list = []
print("simulating....")
for i in range(1, total_sampling):
pid.update(feedback)
output = pid.output
if pid.SetPoint > 0:
feedback += (output - (1 / i))
if 20 < i < 60:
pid.SetPoint = 1
if 60 <= i < 80:
pid.SetPoint = 0.5
if i >= 80:
pid.SetPoint = 1.3
time.sleep(0.02)
feedback_list.append(feedback)
setpoint_list.append(pid.SetPoint)
time_list.append(i)
time_sm = np.array(time_list)
time_smooth = np.linspace(time_sm.min(), time_sm.max(), 300)
feedback_smooth = spline(time_list, feedback_list, time_smooth)
fig1 = plt.gcf()
fig1.subplots_adjust(bottom=0.15)
plt.plot(time_smooth, feedback_smooth, color='red')
plt.plot(time_list, setpoint_list, color='blue')
plt.xlim((0, total_sampling))
plt.ylim((min(feedback_list) - 0.5, max(feedback_list) + 0.5))
plt.xlabel('time (s)')
plt.ylabel('PID (PV)')
plt.title('TEST PID')
plt.grid(True)
print("saving...")
fig1.savefig('result.png', dpi=100)Save this program into a file called test_pid.py. Then, run this program.
$ python test_pid.py
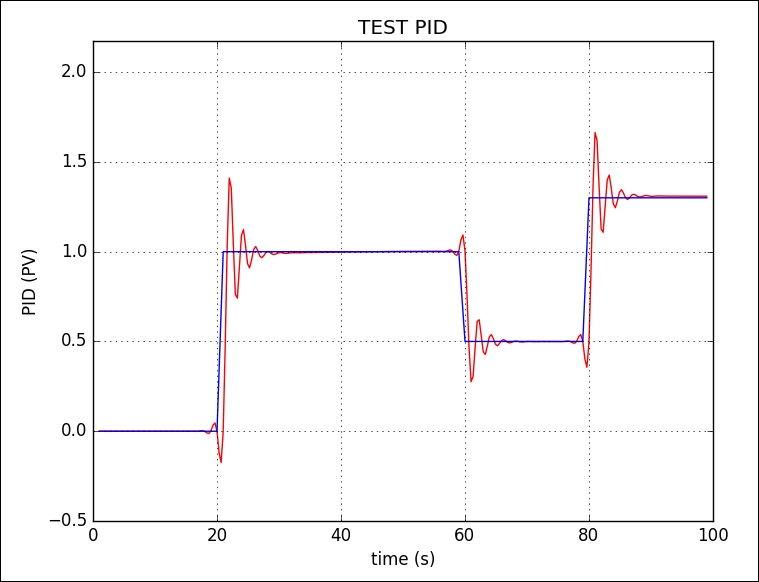
This program will generate result.png as a result of the PID process. A sample of the output form, result.png, is shown in the following figure. You can see that the blue line represents desired values and the red line is an output of PID:
How does it work?
First, we define our PID parameters, as follows:
P = 1.4 I = 1 D = 0.001 pid = PID.PID(P, I, D) pid.SetPoint = 0.0 pid.setSampleTime(0.01) total_sampling = 100 feedback = 0 feedback_list = [] time_list = [] setpoint_list = []
After that, we compute the PID value during sampling time. In this case, we set the desired output value as follows:
- Desired output
1for sampling from 20 to 60 - Desired output
0.5for sampling from 60 to 80 - Desired output
1.3for sampling more than 80for i in range(1, total_sampling): pid.update(feedback) output = pid.output if pid.SetPoint > 0: feedback += (output - (1 / i)) if 20 < i < 60: pid.SetPoint = 1 if 60 <= i < 80: pid.SetPoint = 0.5 if i >= 80: pid.SetPoint = 1.3 time.sleep(0.02) feedback_list.append(feedback) setpoint_list.append(pid.SetPoint) time_list.append(i)
The last step is to generate a report and is saved to a file called result.png:
time_sm = np.array(time_list)
time_smooth = np.linspace(time_sm.min(), time_sm.max(), 300)
feedback_smooth = spline(time_list, feedback_list, time_smooth)
fig1 = plt.gcf()
fig1.subplots_adjust(bottom=0.15)
plt.plot(time_smooth, feedback_smooth, color='red')
plt.plot(time_list, setpoint_list, color='blue')
plt.xlim((0, total_sampling))
plt.ylim((min(feedback_list) - 0.5, max(feedback_list) + 0.5))
plt.xlabel('time (s)')
plt.ylabel('PID (PV)')
plt.title('TEST PID')
plt.grid(True)
print("saving...")
fig1.savefig('result.png', dpi=100)Controlling room temperature using PID controller
Now we can change our PID controller simulation using the real application. We use DHT-22 to check a room temperature. The output of measurement is used as feedback input for the PID controller.
If the PID output positive value, then we turn on heater. Otherwise, we activate cooler machine. It may not good approach but this good point to show how PID controller work.
We attach DHT-22 to GPIO23 (BCM). Let's write the following program:
import matplotlib
matplotlib.use('Agg')
import PID
import Adafruit_DHT
import time
import matplotlib.pyplot as plt
import numpy as np
from scipy.interpolate import spline
sensor = Adafruit_DHT.DHT22
# DHT22 pin on Raspberry Pi
pin = 23
P = 1.4
I = 1
D = 0.001
pid = PID.PID(P, I, D)
pid.SetPoint = 0.0
pid.setSampleTime(0.25) # a second
total_sampling = 100
sampling_i = 0
measurement = 0
feedback = 0
feedback_list = []
time_list = []
setpoint_list = []
print('PID controller is running..')
try:
while 1:
pid.update(feedback)
output = pid.output
humidity, temperature = Adafruit_DHT.read_retry(sensor, pin)
if humidity is not None and temperature is not None:
if pid.SetPoint > 0:
feedback += temperature + output
print('i={0} desired.temp={1:0.1f}*C temp={2:0.1f}*C pid.out={3:0.1f} feedback={4:0.1f}'
.format(sampling_i, pid.SetPoint, temperature, output, feedback))
if output > 0:
print('turn on heater')
elif output < 0:
print('turn on cooler')
if 20 < sampling_i < 60:
pid.SetPoint = 28 # celsius
if 60 <= sampling_i < 80:
pid.SetPoint = 25 # celsius
if sampling_i >= 80:
pid.SetPoint = 20 # celsius
time.sleep(0.5)
sampling_i += 1
feedback_list.append(feedback)
setpoint_list.append(pid.SetPoint)
time_list.append(sampling_i)
if sampling_i >= total_sampling:
break
except KeyboardInterrupt:
print("exit")
print("pid controller done.")
print("generating a report...")
time_sm = np.array(time_list)
time_smooth = np.linspace(time_sm.min(), time_sm.max(), 300)
feedback_smooth = spline(time_list, feedback_list, time_smooth)
fig1 = plt.gcf()
fig1.subplots_adjust(bottom=0.15, left=0.1)
plt.plot(time_smooth, feedback_smooth, color='red')
plt.plot(time_list, setpoint_list, color='blue')
plt.xlim((0, total_sampling))
plt.ylim((min(feedback_list) - 0.5, max(feedback_list) + 0.5))
plt.xlabel('time (s)')
plt.ylabel('PID (PV)')
plt.title('Temperature PID Controller')
plt.grid(True)
fig1.savefig('pid_temperature.png', dpi=100)
print("finish")Save this program to a file called ch01_pid.py. Now you can this program:
$ sudo python ch01_pid.py
After executing the program, you should obtain a file called pid_temperature.png. A sample output of this file can be seen in the following figure:
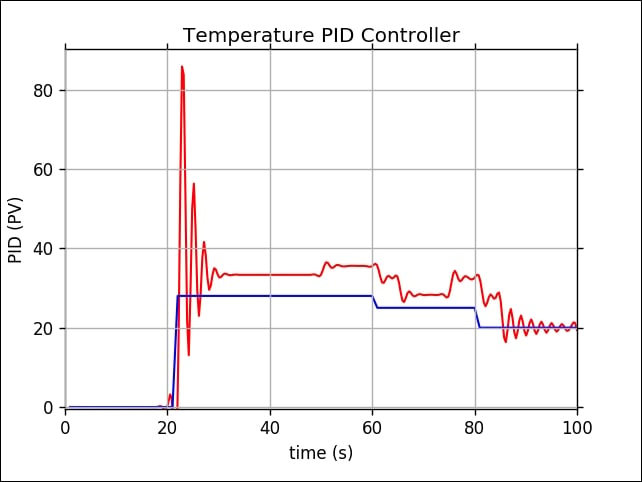
If I don't take any action either turning on a cooler or turning on a heater, I obtain a result, shown in the following figure:
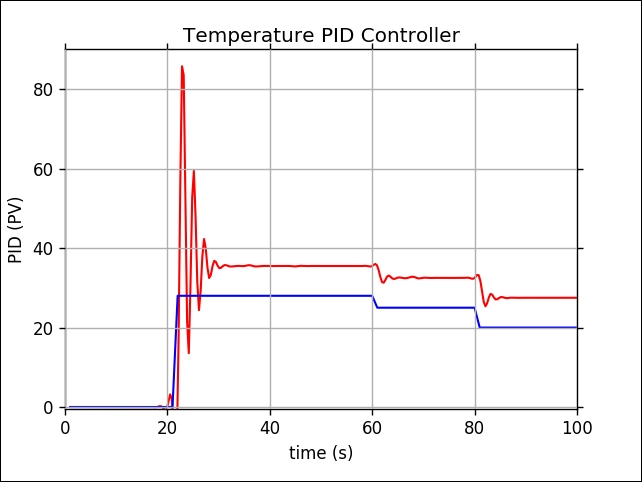
How does it work?
Generally speaking, this program combines our two topics: reading current temperature through DHT-22 and implementing a PID controller. After measuring the temperature, we send this value to the PID controller program. The output of PID will take a certain action. In this case, it will turn on cooler and heater machines.


























































