Introduction
The Markov chain: A sequence of trials of an experiment is a Markov chain if the outcome of each experiment is one of the set of discrete states, and the outcome of the experiment is dependent only on the present state and not of any of the past states. The probability of changing from one state to another state is represented as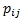
. It is called a transition probability. The transition probability matrix is an n × n matrix such that each element of the matrix is non-negative and each row of the matrix sums to one.
Continuous time Markov chains: Continuous-time Markov chains can be labeled as transition systems augmented with rates that have discrete states. The states have continuous time-steps and the delays are exponentially distributed. Continuous-time Markov chains are suited to model reliability models, control systems, biological pathways, chemical reactions, and so on.
Monte Carlo simulations: Monte Carlo simulation is a stochastic simulation...
