Functions and relations
We are related to different people in different ways; for example, the relationship between a father and his son, the relationship between a teacher and their students, and the relationship between co-workers, to name just a few. Similarly, relationships exist between different elements in mathematics.
Definition: Relations, domains, and ranges
- A relation r between sets X and Y is a set of ordered pairs (x, y) where x
 X and y
X and y  Y.
Y. - The set {x
 X | (x, y)
X | (x, y)  r for some y
r for some y  Y} is the domain of r.
Y} is the domain of r. - The set {y
 Y | (x, y)
Y | (x, y)  r for some x
r for some x  X} is the range of r.
X} is the range of r.
More informally, a relation pairs element of X with one or more elements of Y.
Definition: Functions
- A function f from X to Y, denoted f : X→Y, is a relation that maps each element of X to exactly one element of Y.
- X is the domain of f.
- Elements of the function (x, y) are sometimes written (x, f(x)).
As the definitions reveal, functions are relations, but must satisfy a number of additional assumptions, in other words, every element of X is mapped to exactly 1 element of Y.
Examples: Relations versus functions
Let's look at X = {1, 2, 3, 4, 5} and Y = {2, 4, 6, …}. Consider two relations between X and Y:
- r = {(3, 2), (3, 6), (5, 6)}
- s = {(1, 4), (2, 4), (3, 8), (4, 6), (5, 2)}
The domain of r is {3,5} and the range of r is {2, 6} while the domain of s is all of X and the range of s is {2, 4, 6, 8}.
Relation r is not a function because it maps 3 to both 2 and 6. However, s is a function with domain X since it maps each element of X to exactly one element of Y.
Example: Functions in elementary algebra
Elementary algebra courses tend to focus on specific sorts of functions where the domain and range are intervals of the real number line. Domain values are usually denoted by x and values in the range are denoted by y because the set of ordered pairs (x, y) that satisfy the equation y = f(x) plotted on the Cartesian xy-plane form the graph of the function, as can be seen in the following diagram:
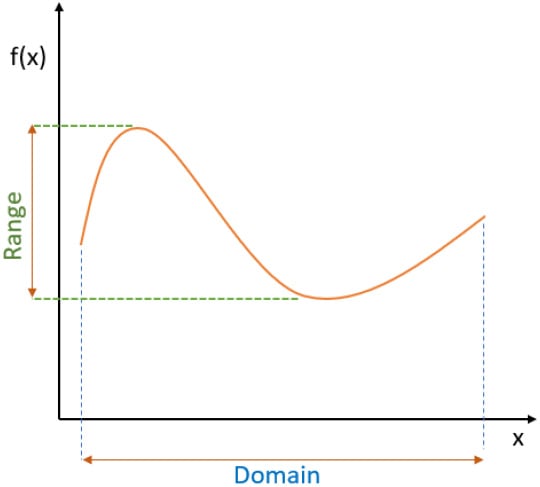
Figure 1.10 – Cartesian xy-plane
While this typical type of functions may be familiar to most readers, the concept of a function is more general than this. First, the input or the output is required to be a number. The domain of a function could consist of any set, so the members of the set may be points in space, graphs, matrices, arrays or strings, or any other types of elements.
In Python and most other programming languages, there are blocks of code known as "functions," which programmers give names and will run when you call them. These Python functions may or may not take inputs (referred to as "parameters") and return outputs, and each set of input parameters may or may not always return the same output. As such, it is important to note Python functions are not necessarily functions in the mathematical sense, although some of them are.
This is an example of conflicting vocabulary in the fields of mathematics and computer science. The next example will discuss some Python functions that are, and some that are not, functions in the mathematical sense.
Example: Python functions versus mathematical functions
Consider the sort() Python function, which is used for sorting lists. See this function applied to two lists – one list of numbers and one list of names:
numbers = [3, 1, 4, 12, 8, 5, 2, 9] names = ['Wyatt', 'Brandon', 'Kumar', 'Eugene', 'Elise'] # Apply the sort() function to the lists numbers.sort() names.sort() # Display the output print(numbers) print(names)
The output is as follows:
[1, 2, 3, 4, 5, 8, 9, 12] ['Brandon', 'Elise', 'Eugene', 'Kumar', 'Wyatt']
In each case, the sort() function sorts the list in ascending order by default (with respect to numerical order or alphabetical order).
Furthermore, we can say that sort() applies to any lists and is a function in the mathematical sense. Indeed, it meets all the criteria:
- The domain is all lists that can be sorted.
- The range is the set of all such lists that have been sorted.
sort()always maps each list that can be inputted to a unique sorted list in the range.
Consider now the Python function random, shuffle(), which takes a list as an input and puts it into a random order. (Just like the shuffle option on your favorite music app!) Refer to the following code:
import random # Set a random seed so the code is reproducible random.seed(1) # Run the random.shuffle() function 5 times and display the # outputs for i in range(0,5): numbers = [3, 1, 4, 12, 8, 5, 2, 9] random.shuffle(numbers) print(numbers)
The output is as follows:
[8, 4, 9, 2, 1, 3, 5, 12] [5, 1, 3, 8, 2, 12, 9, 4] [2, 1, 12, 9, 5, 4, 8, 3] [1, 2, 3, 12, 5, 8, 4, 9] [5, 8, 9, 12, 4, 3, 2, 1]
This code runs a loop where each iteration sets the list numbers to [3, 1, 4, 12, 8, 5, 2, 9], applies the shuffle function to it, and prints the output.
In each iteration, the Python function shuffle() takes the same input, but the output is different each time. Therefore, the Python function shuffle() is not a mathematical function. It is, however, a relation that can pair each list with any ordering of itself.


























































