ARIMA models

In the previous section, we saw the random walk and the role of ACF and PACF functions. The random walk may be seen as a series that depends on past observations as well as past errors. It is thus possible to visualize time series as functions of past observations, errors, or both. In general, given the time series Y_t, 1 < t < T and the error process ε_t, 1 < t < T a linear process is defined as:

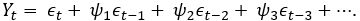
The terms 

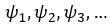
are the coefficients of linear processes. Now, suppose that we are interested in a model where Y _t depends on the past p observations:

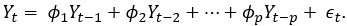
The preceding model is well known as the autoregressive model of order p and it is denoted by AR(p). It is important to note here that the AR coefficients 

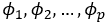
are not unrestricted and we simply note that their absolute values need to be less than 1 if the time series is assumed to be stationary. Next, we define the moving average model of order q, abbreviated as MA(q), as:

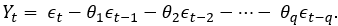
The parameters of the MA(q) model are

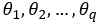
. It is indeed possible...