Convolutional operators
Even if we work only with finite and discrete convolutions, it's useful to start providing the standard definition based on integrable functions. For simplicity, let's suppose that f(t) and k(t) are two real functions of a single variable with support in 
. The convolution of f(t) and k(t) (conventionally denoted as f(t) * k(t)), which we are going to call a kernel, is defined as follows:
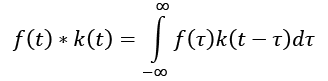
The expression may not be very easy to understand without a mathematical background, but it can become exceptionally simple with a few considerations. First of all, the integral sums all values of 
; therefore, the convolution is a function of the remaining variable, t. The second fundamental element is a sort of dynamic property: the kernel is reversed (
) and transformed into a function of a new variable, 
. Without deep mathematical knowledge, it's possible to understand that this operation shifts the function along the (independent variable) axis...
