Let's consider the following dataset:
We define affinity, a metric function of two arguments with the same dimensionality m. The most common metrics (also supported by scikit-learn) are:
- Euclidean or L2:
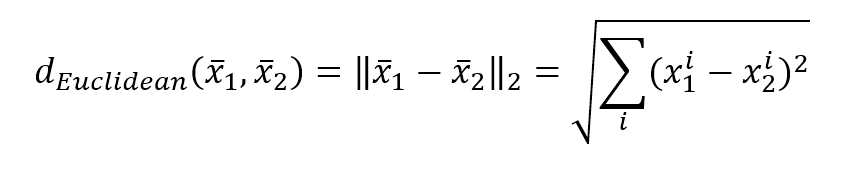
- Manhattan (also known as City Block) or L1:
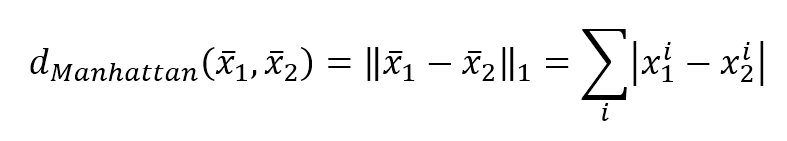
- Cosine distance:
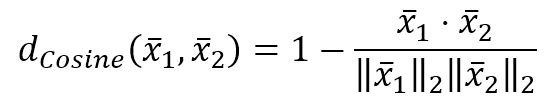
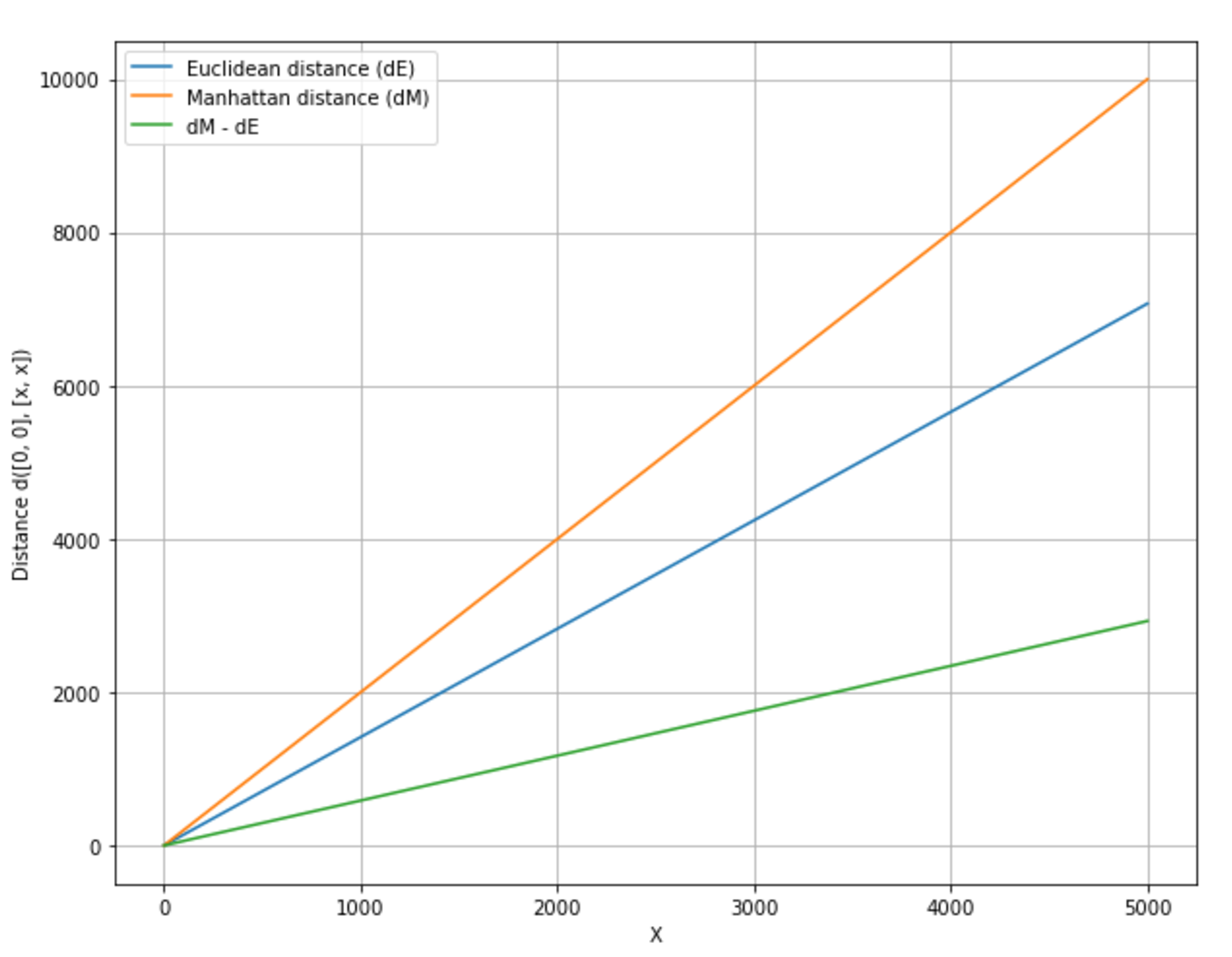
The Euclidean distance is normally a good choice, but sometimes it's useful to a have a metric whose difference with the Euclidean one gets larger and larger. The Manhattan metric has this property; to show it, in the following figure there's a plot representing the distances from the origin of points belonging to the line y = x:
The cosine distance, instead, is useful when we need a distance proportional to the angle between two vectors. If the direction is the same, the distance is null, while it is maximum when the angle is equal to 180° (meaning opposite...


























































