One of the most common ways to reduce the dimensionality of a dataset is based on the analysis of the sample covariance matrix. In general, we know that the information content of a random variable is proportional to its variance. For example, given a multivariate Gaussian, the entropy, which is the mathematical expression that we employ to measure the information, is as follows:
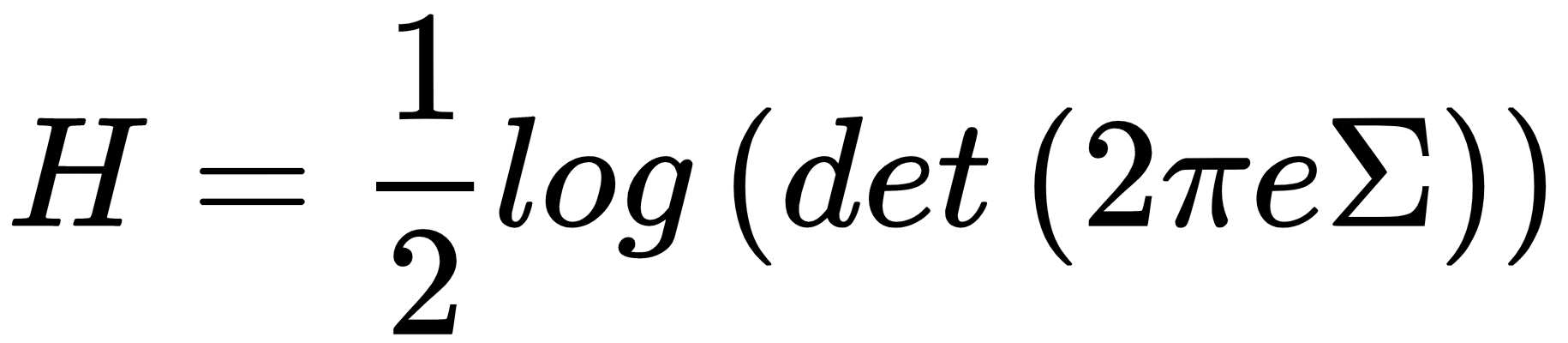
In the previous formula, Σ is the covariance matrix. If we assume (without loss of generality) that Σ is diagonal, it's easy to understand that the entropy is larger (proportionally) than the variance of each single component, σi2. This is not surprising, because a random variable with a low variance is concentrated around the mean, and the probability of surprises is low. On the other hand, when σ2 becomes larger and larger, the potential...
























































