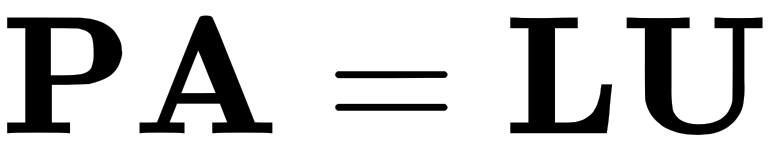Matrix operations

Now that we understand how to solve systems of linear equations of the type where we multiplied a matrix with a column vector, let's move on to dealing with the types of operations we can do with one or more matrices.

Adding matrices

As with scalars and vectors, sometimes we may have to add two or more matrices together, and the process of doing so is rather straightforward. Let's take two matrices, A and B, and add them:

It is important to note that we can only add matrices that have the same dimensions, and, as you have probably noticed, we add the matrices element-wise.

Multiplying matrices

So far, we have only multiplied a matrix by a column vector. But now, we will multiply a matrix A with another matrix B.

There are four simple rules that will help us in multiplying matrices, listed here:

• Firstly, we can only multiply two matrices when the number of columns in matrix A is equal to the number of rows in matrix B.
• Secondly, the first row of matrix A multiplied by the first column of matrix B gives us the first element in the matrix AB, and so on.

• Thirdly, when multiplying, order matters—specifically, AB ≠ BA.
• Lastly, the element at row i, column j is the product of the i^th row of matrix A and the j^th column of matrix B.

Let's multiply an arbitrary 4x5 matrix with an arbitrary 5x6 matrix, as follows:

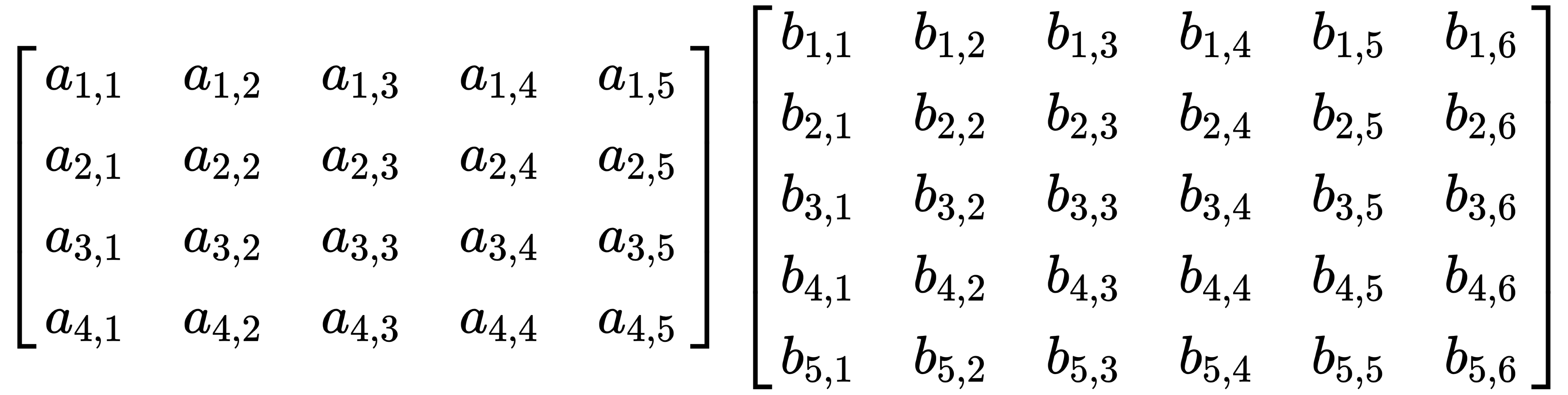
This results in a 4x6 matrix, like this:

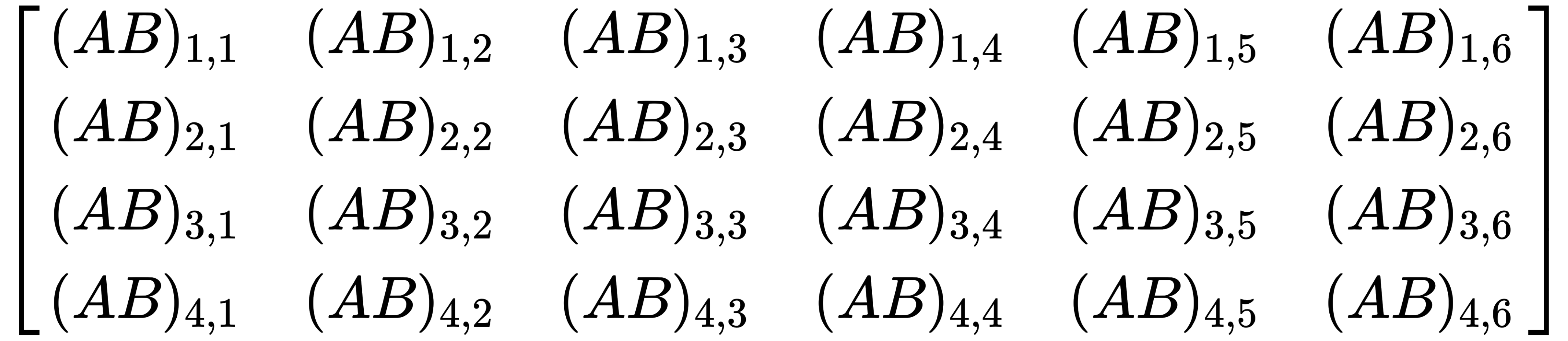
From that, we can deduce that in general, the following applies:

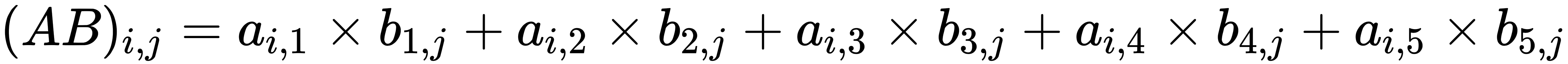
Let's take the following two matrices and multiply them, like this:

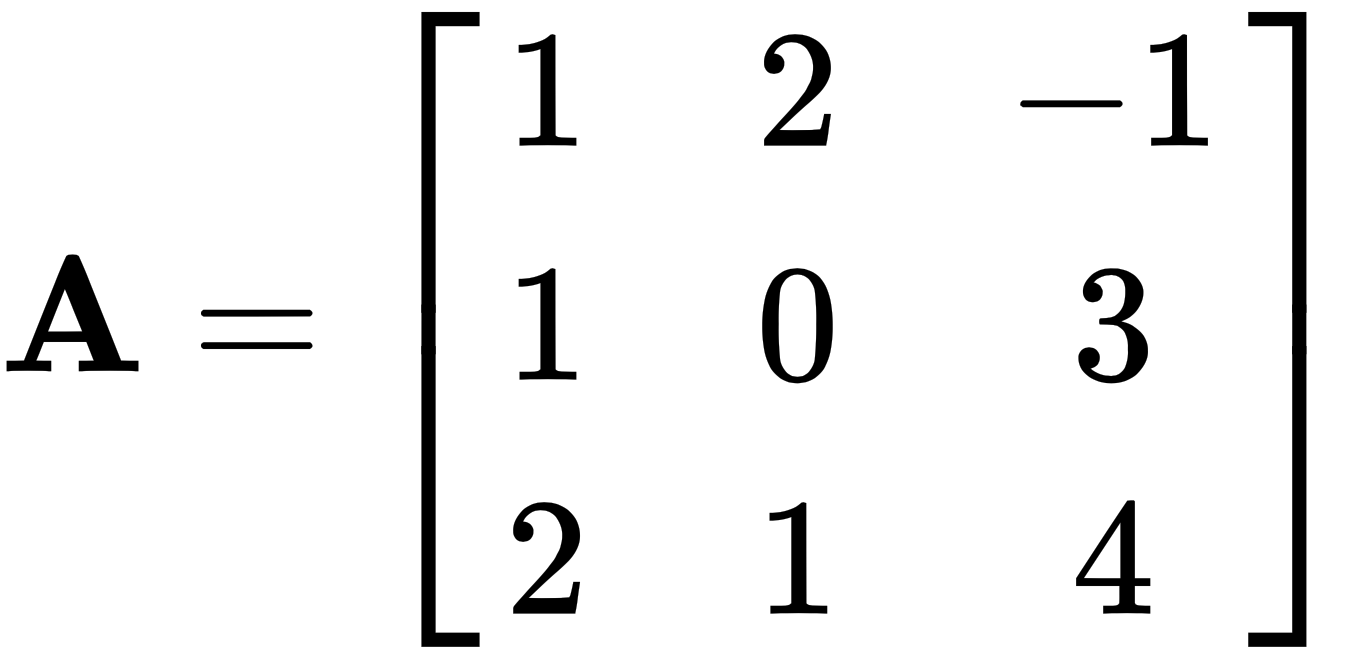and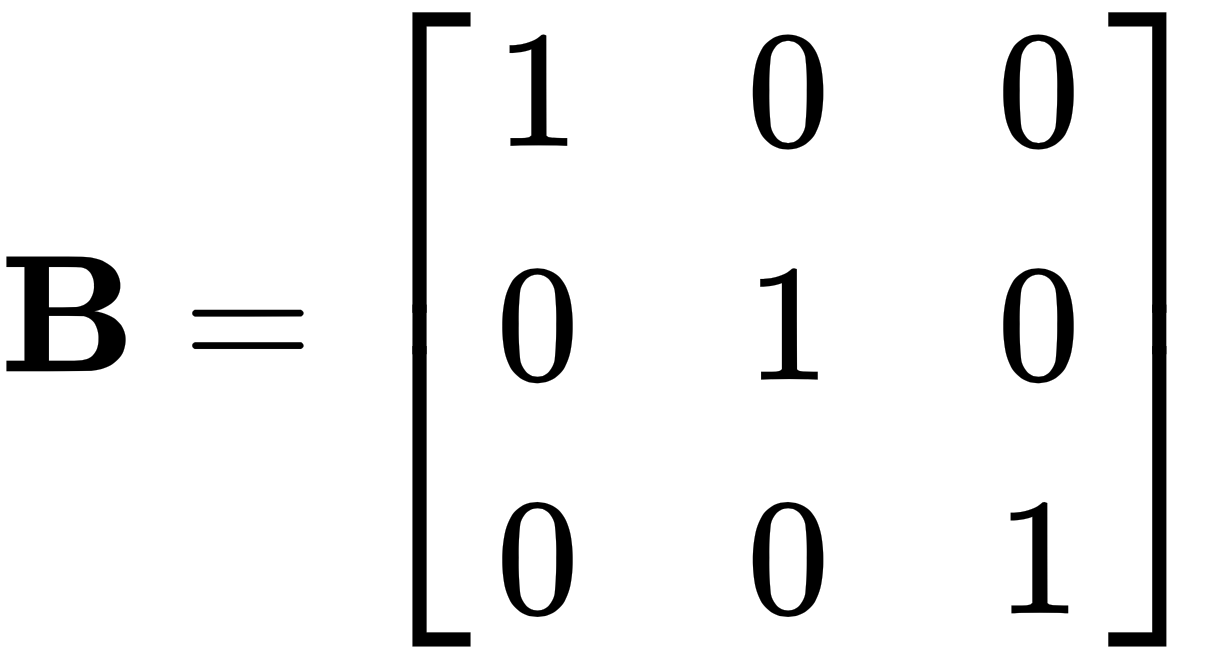

This will give us the following matrix:

.

Note: In this example, the matrix B is the identity matrix, usually written as I.

The identity matrix has two unique properties in matrix multiplication. When multiplied by any matrix, it returns the original matrix unchanged, and the order of multiplication does not matter—so, AI = IA = A.

For example, let's use the same matrix A from earlier, and multiply it by another matrix B, as follows:

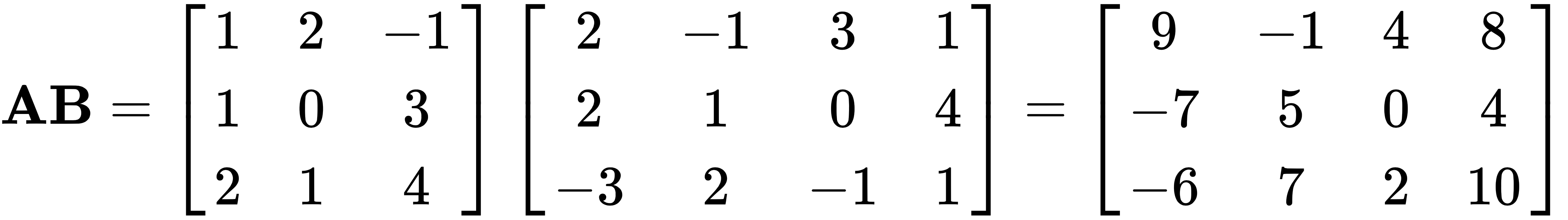
Another very special matrix is the inverse matrix, which is written as A^-1. And when we multiply A with A^-1, we receive I, the identity matrix.

As mentioned before, the order in which we multiply matters. We must keep the matrices in order, but we do have some flexibility. As we can see in the following equation, the parentheses can be moved:

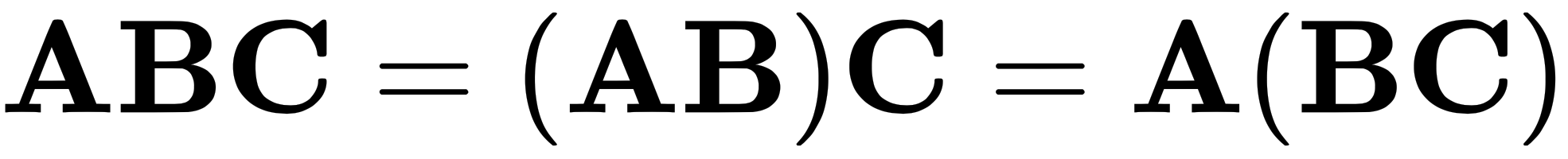
This is the first law of matrix operations, known as associativity.

The following are three important laws that cannot be broken:

• commutativity:
• distributivity: or
• associativity:

As proof that AB ≠ BA, let's take a look at the following example:

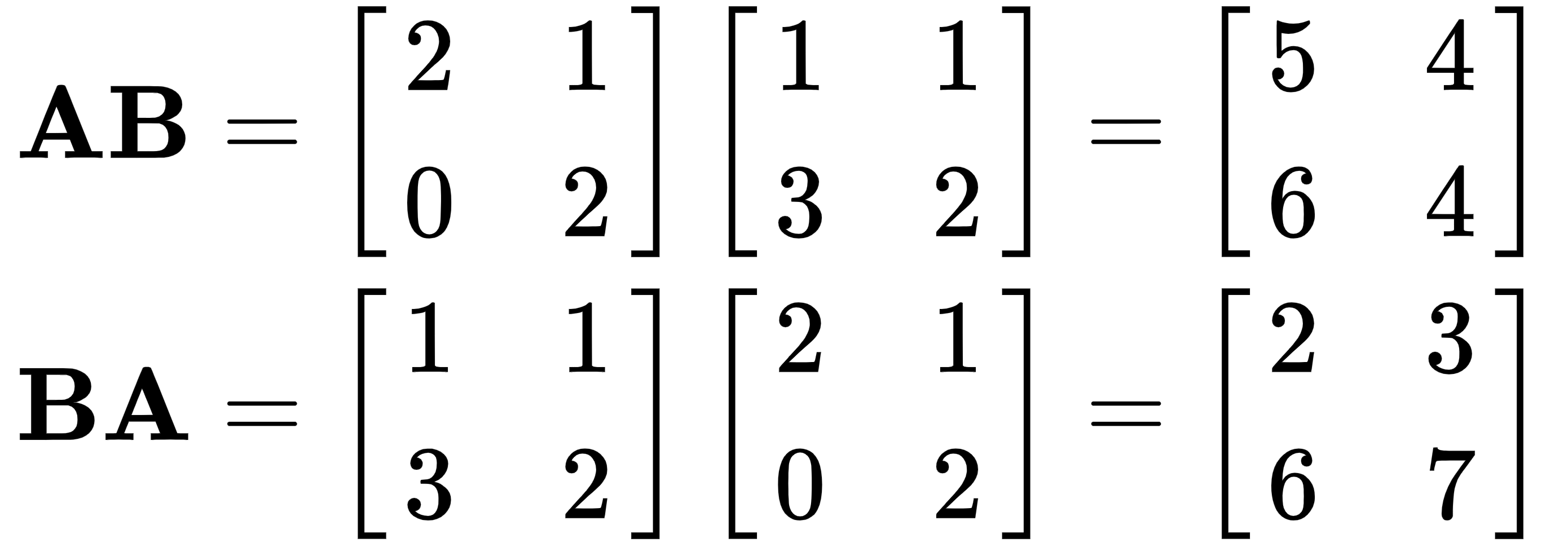
This conclusively shows that the two results are not the same.

We know that we can raise numbers to powers, but we can also raise matrices to powers.

If we raise the matrix A to power p, we get the following:

(multiplying the matrix by itself p times)

There are two additional power laws for matrices— and .

Inverse matrices

Let's revisit the concept of inverse matrices and go a little more in depth with them. We know from earlier that AA^-1 = I, but not every matrix has an inverse.

There are, again, some rules we must follow when it comes to finding the inverses of matrices, as follows:

• The inverse only exists if, through the process of upper or lower triangular factorization, we obtain all the pivot values on the diagonal.
• If the matrix is invertible, it has only one unique inverse matrix—that is, if AB = I and AC = I, then B = C.
• If A is invertible, then to solve Av = b we multiply both sides by A^-1 and get AA^-1v = A^-1b, which finally gives us = A^-1b.
• If v is nonzero and b = 0, then the matrix does not have an inverse.
• 2 x 2 matrices are invertible only if ad - bc ≠ 0, where the following applies:

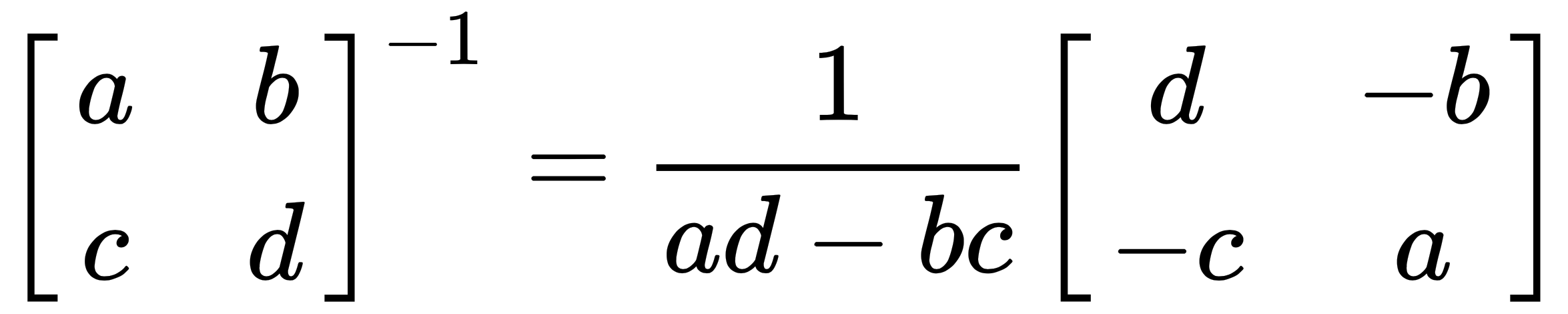
And ad - bc is called the determinant of A. A^-1 involves dividing each element in the matrix by the determinant.

• Lastly, if the matrix has any zero values along the diagonal, it is non-invertible.

Sometimes, we may have to invert the product of two matrices, but that is only possible when both the matrices are individually invertible (follow the rules outlined previously).

For example, let's take two matrices A and B, which are both invertible. Then, so that .

Note: Pay close attention to the order of the inverse—it too must follow the order. The left-hand side is the mirror image of the right-hand side.

Matrix transpose

Let's take an matrix A. If the matrix's transpose is B, then the dimensions of B are , such that: . Here is the matrix A:

Then, the matrix B is as given:

.

Essentially, we can think of this as writing the columns of A as the rows of the transposed matrix, B.

We usually write the transpose of A as A^T.

A symmetric matrix is a special kind of matrix. It is an n×n matrix that, when transposed, is exactly the same as before we transposed it.

The following are the properties of inverses and transposes:

• 
• 
• 

• 
• 
• 

If A is an invertible matrix, then so is A^T, and so (A^-1)^T = (A^T)^-1 = A^-T.

Permutations

In the example on solving systems of linear equations, we swapped the positions of rows 2 and 3. This is known as a permutation.

When we are doing triangular factorization, we want our pivot values to be along the diagonal of the matrix, but this won't happen every time—in fact, it usually won't. So, instead, what we do is swap the rows so that we get our pivot values where we want them.

But that is not their only use case. We can also use them to scale individual rows by a scalar value or add rows to or subtract rows from other rows.

Let's start with some of the more basic permutation matrices that we obtain by swapping the rows of the identity matrix. In general, we have n! possible permutation matrices that can be formed from an nxn identity matrix. In this example, we will use a 3×3 matrix and therefore have six permutation matrices, and they are as follows:

• This matrix makes no change to the matrix it is applied on.
• This matrix swaps rows two and three of the matrix it is applied on.
• This matrix swaps rows one and two of the matrix it is applied on.

• This matrix shifts rows two and three up one and moves row one to the position of row three of the matrix it is applied on.
• This matrix shifts rows one and two down one and moves row three to the row-one position of the matrix it is applied on.
• This matrix swaps rows one and three of the matrix it is applied on.

It is important to note that there is a particularly fascinating property of permutation matrices that states that if we have a matrix and it is invertible, then there exists a permutation matrix that when applied to A will give us the LU factor of A. We can express this like so: