Chapter 5: Mastering Structured Data

Activity 14: Training and Predicting the Income of a Person

Solution:

1. Import the libraries and load the income dataset using pandas. First, import pandas and then read the data using read_csv.

   import pandas as pd

   import xgboost as xgb

   import numpy as np

   from sklearn.metrics import accuracy_score

   data = pd.read_csv("../data/adult-data.csv", names=['age', 'workclass', 'education-num', 'occupation', 'capital-gain', 'capital-loss', 'hours-per-week', 'income'])

   The reason we are passing the names of the columns is because the data doesn't contain them. We do this to make our lives easy.

2. Use Label Encoder from sklearn to encode strings. First, import Label Encoder. Then, encode all string categorical columns one by one.

   from sklearn.preprocessing import LabelEncoder

   data['workclass'] = LabelEncoder().fit_transform(data['workclass'])

   data['occupation'] = LabelEncoder().fit_transform(data['occupation'])

   data['income'] = LabelEncoder().fit_transform(data['income'])

   Here, we encode all the categorical string data that we have. There is another method we can use to prevent writing the same piece of code again and again. See if you can find it.

3. We first separate the dependent and independent variables.

   X = data.copy()

   X.drop("income", inplace = True, axis = 1)

   Y = data.income

4. Then, we divide them into training and testing sets with an 80:20 split.

   X_train, X_test = X[:int(X.shape[0]*0.8)].values, X[int(X.shape[0]*0.8):].values

   Y_train, Y_test = Y[:int(Y.shape[0]*0.8)].values, Y[int(Y.shape[0]*0.8):].values

5. Next, we convert them into DMatrix, a data structure that the library supports.

   train = xgb.DMatrix(X_train, label=Y_train)

   test = xgb.DMatrix(X_test, label=Y_test)

6. Then, we use the following parameters to train the model using XGBoost.

   param = {'max_depth':7, 'eta':0.1, 'silent':1, 'objective':'binary:hinge'} num_round = 50

   model = xgb.train(param, train, num_round)

7. Check the accuracy of the model.

   preds = model.predict(test)

   accuracy = accuracy_score(Y[int(Y.shape[0]*0.8):].values, preds)

   print("Accuracy: %.2f%%" % (accuracy * 100.0))

   The output is as follows:

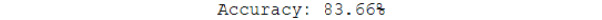
Figure 5.36: Final model accuracy

Activity 15: Predicting the Loss of Customers

Solution:

1. Load the income dataset using pandas. First, import pandas, and then read the data using read_csv.

   import pandas as pd

   import numpy as np

   data = data = pd.read_csv("data/telco-churn.csv")

2. The customerID variable is not required because any future prediction will have a unique customerID, making this variable useless for prediction.

   data.drop('customerID', axis = 1, inplace = True)

3. Convert all categorical variables to integers using scikit. One example is given below.

   from sklearn.preprocessing import LabelEncoder

   data['gender'] = LabelEncoder().fit_transform(data['gender'])

4. Check the data types of the variables in the dataset.

   data.dtypes

   The data types of the variables will be shown as follows:

   

   Figure 5.37: Data types of variables

5. As you can see, TotalCharges is an object. So, convert the data type of TotalCharges from object to numeric. coerce will make the missing values null.

   data.TotalCharges = pd.to_numeric(data.TotalCharges, errors='coerce')

6. Convert the data frame to an XGBoost variable and find the best parameters for the dataset using the previous exercises as reference.

   import xgboost as xgb

   import matplotlib.pyplot as plt

   X = data.copy()

   X.drop("Churn", inplace = True, axis = 1)

   Y = data.Churn

   X_train, X_test = X[:int(X.shape[0]*0.8)].values, X[int(X.shape[0]*0.8):].values

   Y_train, Y_test = Y[:int(Y.shape[0]*0.8)].values, Y[int(Y.shape[0]*0.8):].values

   train = xgb.DMatrix(X_train, label=Y_train)

   test = xgb.DMatrix(X_test, label=Y_test)

   test_error = {}

   for i in range(20):

       param = {'max_depth':i, 'eta':0.1, 'silent':1, 'objective':'binary:hinge'}

       num_round = 50

       model_metrics = xgb.cv(param, train, num_round, nfold = 10)

       test_error[i] = model_metrics.iloc[-1]['test-error-mean']

   plt.scatter(test_error.keys(),test_error.values())

   plt.xlabel('Max Depth')

   plt.ylabel('Test Error')

   plt.show()

   Check out the output in the following screenshot:

   

   Figure 5.38: Graph of max depth to test error for telecom churn dataset

   From the graph, it is clear that a max depth of 4 gives the least error. So, we will be using that to train our model.

7. Create the model using the max_depth parameter that we chose from the previous steps.

   param = {'max_depth':4, 'eta':0.1, 'silent':1, 'objective':'binary:hinge'}

   num_round = 100

   model = xgb.train(param, train, num_round)

   preds = model.predict(test)

   from sklearn.metrics import accuracy_score

   accuracy = accuracy_score(Y[int(Y.shape[0]*0.8):].values, preds)

   print("Accuracy: %.2f%%" % (accuracy * 100.0))

   The output is as follows:

   

   Figure 5.39: Final accuracy

8. Save the model for future use using the following code:

   model.save_model('churn-model.model')

Activity 16: Predicting a Customer's Purchase Amount

Solution:

1. Load the Black Friday dataset using pandas. First, import pandas, and then, read the data using read_csv.

   import pandas as pd

   import numpy as np

   data = data = pd.read_csv("data/BlackFriday.csv")

2. The User_ID variable is not required to allow predictions on new user Ids, so we drop it.

   data.isnull().sum()

   data.drop(['User_ID', 'Product_Category_2', 'Product_Category_3'], axis = 1, inplace = True)

   The product category variables have high null values, so we drop them as well.

3. Convert all categorical variables to integers using scikit-learn.

   from collections import defaultdict

   from sklearn.preprocessing import LabelEncoder, MinMaxScaler

   label_dict = defaultdict(LabelEncoder)

   data[['Product_ID', 'Gender', 'Age', 'Occupation', 'City_Category', 'Stay_In_Current_City_Years', 'Marital_Status', 'Product_Category_1']] = data[['Product_ID', 'Gender', 'Age', 'Occupation', 'City_Category', 'Stay_In_Current_City_Years', 'Marital_Status', 'Product_Category_1']].apply(lambda x: label_dict[x.name].fit_transform(x))

4. Split the data into training and testing sets and convert it into the form required by the embedding layers.

   from sklearn.model_selection import train_test_split

   X = data

   y = X.pop('Purchase')

   X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=9)

    

   cat_cols_dict = {col: list(data[col].unique()) for col in ['Product_ID', 'Gender', 'Age', 'Occupation', 'City_Category', 'Stay_In_Current_City_Years', 'Marital_Status', 'Product_Category_1']}

   train_input_list = []

   test_input_list = []

    

   for col in cat_cols_dict.keys():

       raw_values = np.unique(data[col])

       value_map = {}

       for i in range(len(raw_values)):

           value_map[raw_values[i]] = i

       train_input_list.append(X_train[col].map(value_map).values)

       test_input_list.append(X_test[col].map(value_map).fillna(0).values)

5. Create the network using the embedding and dense layers in Keras and perform hyperparameter tuning to get the best accuracy.

   from keras.models import Model

   from keras.layers import Input, Dense, Concatenate, Reshape, Dropout

   from keras.layers.embeddings import Embedding

   cols_out_dict = {

       'Product_ID': 20,

       'Gender': 1,

       'Age': 2,

       'Occupation': 6,

       'City_Category': 1,

       'Stay_In_Current_City_Years': 2,

       'Marital_Status': 1,

       'Product_Category_1': 9

   }

    

   inputs = []

   embeddings = []

    

   for col in cat_cols_dict.keys():

    

       inp = Input(shape=(1,), name = 'input_' + col)

       embedding = Embedding(len(cat_cols_dict[col]), cols_out_dict[col], input_length=1, name = 'embedding_' + col)(inp)

       embedding = Reshape(target_shape=(cols_out_dict[col],))(embedding)

       inputs.append(inp)

       embeddings.append(embedding)

6. Now, we create a three-layer network after the embedding layers.

   x = Concatenate()(embeddings)

   x = Dense(4, activation='relu')(x)

   x = Dense(2, activation='relu')(x)

   output = Dense(1, activation='relu')(x)

    

   model = Model(inputs, output)

    

   model.compile(loss='mae', optimizer='adam')

    

   model.fit(train_input_list, y_train, validation_data = (test_input_list, y_test), epochs=20, batch_size=128)

7. Check the RMSE of the model on the test set.

   from sklearn.metrics import mean_squared_error

   y_pred = model.predict(test_input_list)

   np.sqrt(mean_squared_error(y_test, y_pred))

   The RMSE is:

   

   Figure 5.40: RMSE model

8. Visualize the product ID embedding.

   import matplotlib.pyplot as plt

   from sklearn.decomposition import PCA

   embedding_Product_ID = model.get_layer('embedding_Product_ID').get_weights()[0]

   pca = PCA(n_components=2)

   Y = pca.fit_transform(embedding_Product_ID[:40])

   plt.figure(figsize=(8,8))

   plt.scatter(-Y[:, 0], -Y[:, 1])

   for i, txt in enumerate(label_dict['Product_ID'].inverse_transform(cat_cols_dict['Product_ID'])[:40]):

       plt.annotate(txt, (-Y[i, 0],-Y[i, 1]), xytext = (-20, 8), textcoords = 'offset points')

   plt.show()

   The plot is as follows:

   

   Figure 5.41: Plot of clustered model

   From the plot, you can see that similar products have been clustered together by the model.

9. Save the model for future use.

   model.save ('black-friday.model')