A brief history and a panoramic overview of cryptographic algorithms
Nobody probably knows which cryptogram was the first to be invented. Cryptography has been used for a long time, approximately 4,000 years, and it has changed its paradigms a lot. First, it was a kind of hidden language, then cryptography was based on a transposition of letters in a mechanical fashion, then finally, mathematics and logic were used to solve complicated problems. What will the future hold? Probably, new methods will be invented to hide our secrets: quantum cryptography, for example, is already being experimented with and will come soon. I will explain new algorithms and methods throughout this book, but let me use this section to show you some interesting ciphers related to the classical period. Despite the computation power we have now, some of these algorithms have not yet been broken.
Rosetta Stone
One of the first extraordinary examples of cryptography was hieroglyphics. Cryptography means hidden words and comes from the union of two Greek words: κρυπτός (crypto) and γράφω (graphy). Among the many definitions of this word, we find the following: converting ordinary plaintext into unintelligible text and vice versa. So, we can include hieroglyphics in this definition, because we discovered how to re-convert their hidden meaning into intelligible text only after the Rosetta Stone was found. As you will probably remember from elementary school, the Rosetta Stone was written in three different languages: Ancient Egyptian (using hieroglyphics), Demotic, and Ancient Greek. The Rosetta Stone could only be decrypted because Ancient Greek was well known at the time:

Figure 1.5 – Rosetta Stone with the three languages detected
Hieroglyphics were a form of communication between the people of a country. The same problem of deciphering an unknown language could occur in the future if and when we get in contact with an alien population. A project called SETI (https://www.seti.org/) focuses on this: "From microbes to alien intelligence, the SETI Institute is America's only organization wholly dedicated to searching for life in the universe." Maybe if one day we get in contact with alien creatures, we will eventually understand their language. You can imagine that hieroglyphics (at the time) appeared as impenetrable as an alien language for someone who had never encountered this form of communication.
Caesar cipher
Continuing our journey through history, we find that during the Roman Empire, cryptography was used to transmit messages from the generals to the commanders and to soldiers. In fact, we find the famous Caesar cipher. Why is this encrypting method so famous in the history of cryptography?
This is not only because it was used by Caesar, who was one of the most valorous Roman statesmen/generals, but also because this method was probably the first that implemented mathematics.
This cipher is widely known as a shift cipher. The technique of shifting is very simple: just shift each letter you want to encrypt a fixed number of places in the alphabet so that the final effect will be to obtain a substitution of each letter for another one. So, for example, if I decide to shift by three letters, then A will become D, E becomes H, and so on.
For example, in this case, by shifting each letter three places, implicitly we have created a secret cryptographic key of [K=3]:
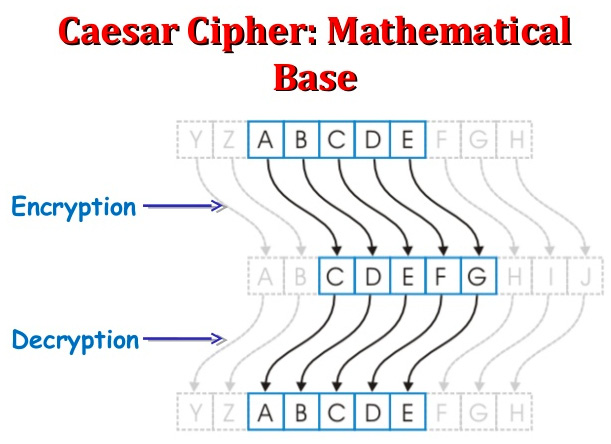
Figure 1.6 – The transposition of the letters in the Caesar cipher during the encryption and decryption processes
It is obviously a symmetric key encryption method. In this case, the algorithm works in the following way:
- Use this key:
(+3). - Message:
HELLO. - To encrypt: Take every letter and shift by
+3steps. - To decrypt: Take every letter and de-shift by
-3.
You can see in the following figure how the process of encryption and decryption of the Caesar algorithm works using key = +3; as you'll notice, the word HELLO becomes KHOOR after encryption, and then it returns to HELLO after decryption:
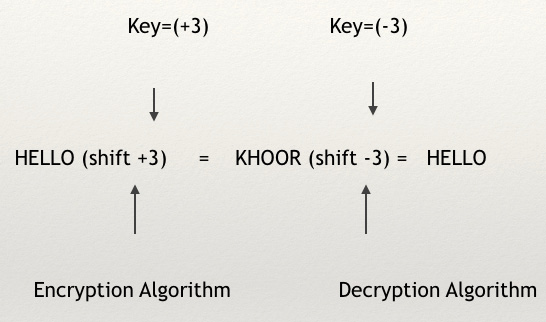
Figure 1.7 – Encryption and decryption using Caesar's algorithm
As you can imagine, the Caesar algorithm is very easy to break with a normal computer if we set a fixed key, as in the preceding example. The scheme is very simple, which, for a cryptographic algorithm, is not a problem. However, the main problem is the extreme linearity of the underlying mathematics. Using a brute-force method, that is, a test that tries all the combinations to discover the key after having guessed the algorithm used (in this case, the shift cipher), we can easily break the code. We have to check at most 25 combinations: all the letters of the English alphabet (26) minus one (that is, the same intelligible plaintext form). This is nothing compared to the billions and billions of attempts that a computer has to make in order to break a modern cryptographic algorithm.
However, there is a more complex version of this algorithm that enormously increases the efficiency of the encryption.
If I change the key for each letter and I use that key to substitute the letters and generate the ciphertext, then things become very interesting.
Let's see what happens if we encrypt HELLO using a method like this:
- Write out the alphabet.
- Choose a passphrase (also known as a keyphrase) such as
[JULIUSCAESAR]and repeat it, putting each letter of the alphabet in correspondence with a character from the passphrase in the second row, as shown in the following screenshot. - After we have defined the message to encrypt, for each character composing the message (in the first row) select the corresponding character of the keyphrase (in the second row).
- Pick up the selected corresponding characters in the second row to create the ciphertext.
Finding it a little bit complicated? Don't worry, the following example will clarify everything.
Let's encrypt HELLO with the keyphrase [JULIUSCAESARJULIUS…]:

Figure 1.8 – Encrypting HELLO with a keyphrase becomes harder to attack
Thus, encrypting the plaintext HELLO using the alphabet and a key (or better, a passphrase or a keyphrase), JULIUSCAESAR, repeated without any spaces, we obtain the correspondent ciphertext: AURRL.
So, H becomes A, E becomes U, L becomes R (twice), and O becomes L.
Earlier, we only had to check 25 combinations to find the key in the Caesar cipher; here, things have changed a little bit, and there are 26 possibilities to discover the key! That means multiply 1*2*3...*26, which results in 403,291,461,126,605,635,584,000,000. This is a very big number. In fact, it is about one-third of all the atoms in the universe. Computationally, it is pretty hard to discover the key, even for a modern computer using a brute-force method.
Another advantage of building a cryptogram like this is that it is easy to memorize the keyword or keyphrase and hence work out the ciphertext. But let's see a cipher that is performed with a similar technique and is used in commercial contexts.
ROT13
A modern example of an algorithm that is used on the internet is ROT13. Essentially, this is a simple cipher derived from the Caesar cipher with a shift of (+13). Computationally, it is easy to break the Caesar cipher, but it yields an interesting effect: if we shift to the left or to the right, we will have the same result.
Just like the preceding example, in ROT13, we have to select letters that correspond to the pre-selected key. Essentially, the difference here is that instead of applying a keyphrase to perform the ciphertext, we will use 13 letters from the English alphabet as the key generator. ROT13 takes in encryption only the letters that occur in the English alphabet and not numbers, symbols, or other characters, which are left as they are. The ROT13 function essentially encrypts the plaintext with a key determined by the first 13 letters transposed into the second 13 letters, and the inverse for the second 13 letters.
Take a look at the following example to better understand the encryption scheme:
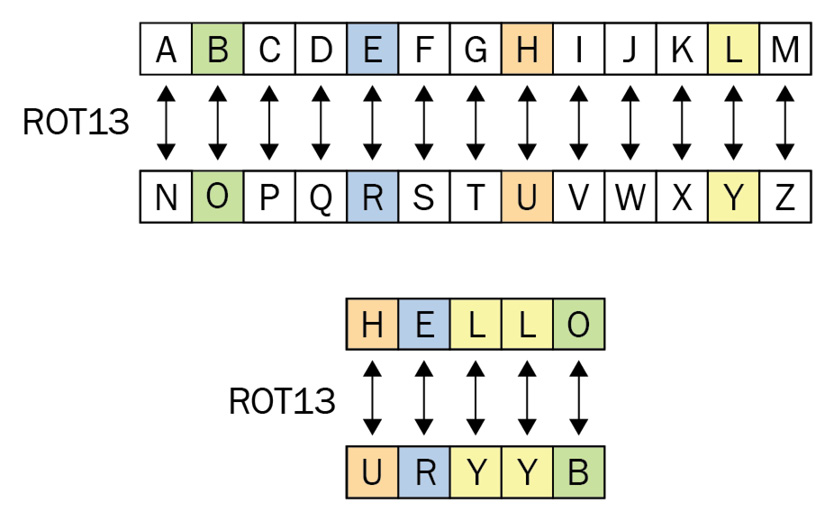
Figure 1.9 – The encryption scheme in ROT13
As you can see in the preceding diagram, H becomes U, E becomes R, L becomes Y (twice), and O becomes B:
HELLO = URYYB
The key consists of the first 13 letters of the alphabet up to M, which becomes Z, then the sequence wraps back to N, which becomes A, O becomes B, and so on to Z, which becomes M.
ROT13 was used to hide potentially offensive jokes or obscure an answer in the net.jokes newsgroup in the early 1980s.
Also, even though ROT13 is not intended to be used for a high degree of secrecy, it is still used in some cases to hide email addresses from unsophisticated spambots. ROT13 is also used for the scope of circumventing spam filters such as obscuring email content. This last function is not recommended because of the extreme vulnerability of this algorithm.
However, ROT13 was used by Netscape Communicator – the browser organization that released https://www.mozilla.org – to store email passwords. Moreover, ROT13 is used in Windows XP to hide some registry keys, so you can understand how sometimes even big corporations can have a lack of security and privacy in communications.
The Beale cipher
Going back to the history of cryptography, I would like to show you an amazing method of encryption whose cipher has not been decrypted yet, despite the immense computational power of our modern calculators. Very often, cryptography is used to hide precious information or fascinating treasure, just as in the mysterious story that lies behind the Beale cipher.
In order to better understand the method of encryption adopted in this cipher, I think it is interesting to know the story (or legend) of Beale and his treasure.
The story involves buried treasure with a value of more than $20 million, a mysterious set of encrypted documents, Wild West cowboys, and a hotel owner who dedicated his life to struggling with the decryption of these papers. The whole story is contained in a pamphlet that was published in 1885.
The story (you can find the whole version here: http://www.unmuseum.org/bealepap.htm) begins in January 1820 in Lynchburg, Virginia at the Washington Hotel where a man named Thomas J. Beale checked in. The owner of the hotel, Robert Morriss, and Beale became friends, and because Mr. Morriss was considered a trustworthy man, he received a box containing three mysterious papers covered in numbers.
After countless troubles and many years of struggle, only the second of the three encrypted papers was deciphered.
What exactly does Beale's cipher look like?
The following content consists of three pages, containing only numbers, in an apparently random order.
The first paper is as follows:
71, 194, 38, 1701, 89, 76, 11, 83, 1629, 48, 94, 63, 132, 16, 111, 95, 84, 341, 975, 14, 40, 64, 27, 81, 139, 213, 63, 90, 1120, 8, 15, 3, 126, 2018, 40, 74, 758, 485, 604, 230, 436, 664, 582, 150, 251, 284, 308, 231, 124, 211, 486, 225, 401, 370, 11, 101, 305, 139, 189, 17, 33, 88, 208, 193, 145, 1, 94, 73, 416, 918, 263, 28, 500, 538, 356, 117, 136, 219, 27, 176, 130, 10, 460, 25, 485, 18, 436, 65, 84, 200, 283, 118, 320, 138, 36, 416, 280, 15, 71, 224, 961, 44, 16, 401, 39, 88, 61, 304, 12, 21, 24, 283, 134, 92, 63, 246, 486, 682, 7, 219, 184, 360, 780, 18, 64, 463, 474, 131, 160, 79, 73, 440, 95, 18, 64, 581, 34, 69, 128, 367, 460, 17, 81, 12, 103, 820, 62, 116, 97, 103, 862, 70, 60, 1317, 471, 540, 208, 121, 890, 346, 36, 150, 59, 568, 614, 13, 120, 63, 219, 812, 2160, 1780, 99, 35, 18, 21, 136, 872, 15, 28, 170, 88, 4, 30, 44, 112, 18, 147, 436, 195, 320, 37, 122, 113, 6, 140, 8, 120, 305, 42, 58, 461, 44, 106, 301, 13, 408, 680, 93, 86, 116, 530, 82, 568, 9, 102, 38, 416, 89, 71, 216, 728, 965, 818, 2, 38, 121, 195, 14, 326, 148, 234, 18, 55, 131, 234, 361, 824, 5, 81, 623, 48, 961, 19, 26, 33, 10, 1101, 365, 92, 88, 181, 275, 346, 201, 206, 86, 36, 219, 324, 829, 840, 64, 326, 19, 48, 122, 85, 216, 284, 919, 861, 326, 985, 233, 64, 68, 232, 431, 960, 50, 29, 81, 216, 321, 603, 14, 612, 81, 360, 36, 51, 62, 194, 78, 60, 200, 314, 676, 112, 4, 28, 18, 61, 136, 247, 819, 921, 1060, 464, 895, 10, 6, 66, 119, 38, 41, 49, 602, 423, 962, 302, 294, 875, 78, 14, 23, 111, 109, 62, 31, 501, 823, 216, 280, 34, 24, 150, 1000, 162, 286, 19, 21, 17, 340, 19, 242, 31, 86, 234, 140, 607, 115, 33, 191, 67, 104, 86, 52, 88, 16, 80, 121, 67, 95, 122, 216, 548, 96, 11, 201, 77, 364, 218, 65, 667, 890, 236, 154, 211, 10, 98, 34, 119, 56, 216, 119, 71, 218, 1164, 1496, 1817, 51, 39, 210, 36, 3, 19, 540, 232, 22, 141, 617, 84, 290, 80, 46, 207, 411, 150, 29, 38, 46, 172, 85, 194, 39, 261, 543, 897, 624, 18, 212, 416, 127, 931, 19, 4, 63, 96, 12, 101, 418, 16, 140, 230, 460, 538, 19, 27, 88, 612, 1431, 90, 716, 275, 74, 83, 11, 426, 89, 72, 84, 1300, 1706, 814, 221, 132, 40, 102, 34, 868, 975, 1101, 84, 16, 79, 23, 16, 81, 122, 324, 403, 912, 227, 936, 447, 55, 86, 34, 43, 212, 107, 96, 314, 264, 1065, 323, 428, 601, 203, 124, 95, 216, 814, 2906, 654, 820, 2, 301, 112, 176, 213, 71, 87, 96, 202, 35, 10, 2, 41, 17, 84, 221, 736, 820, 214, 11, 60, 760
The second paper (which was decrypted) is as follows:
115, 73, 24, 807, 37, 52, 49, 17, 31, 62, 647, 22, 7, 15, 140, 47, 29, 107, 79, 84, 56, 239, 10, 26, 811, 5, 196, 308, 85, 52, 160, 136, 59, 211, 36, 9, 46, 316, 554, 122, 106, 95, 53, 58, 2, 42, 7, 35, 122, 53, 31, 82, 77, 250, 196, 56, 96, 118, 71, 140, 287, 28, 353, 37, 1005, 65, 147, 807, 24, 3, 8, 12, 47, 43, 59, 807, 45, 316, 101, 41, 78, 154, 1005, 122, 138, 191, 16, 77, 49, 102, 57, 72, 34, 73, 85, 35, 371, 59, 196, 81, 92, 191, 106, 273, 60, 394, 620, 270, 220, 106, 388, 287, 63, 3, 6, 191, 122, 43, 234, 400, 106, 290, 314, 47, 48, 81, 96, 26, 115, 92, 158, 191, 110, 77, 85, 197, 46, 10, 113, 140, 353, 48, 120, 106, 2, 607, 61, 420, 811, 29, 125, 14, 20, 37, 105, 28, 248, 16, 159, 7, 35, 19, 301, 125, 110, 486, 287, 98, 117, 511, 62, 51, 220, 37, 113, 140, 807, 138, 540, 8, 44, 287, 388, 117, 18, 79, 344, 34, 20, 59, 511, 548, 107, 603, 220, 7, 66, 154, 41, 20, 50, 6, 575, 122, 154, 248, 110, 61, 52, 33, 30, 5, 38, 8, 14, 84, 57, 540, 217, 115, 71, 29, 84, 63, 43, 131, 29, 138, 47, 73, 239, 540, 52, 53, 79, 118, 51, 44, 63, 196, 12, 239, 112, 3, 49, 79, 353, 105, 56, 371, 557, 211, 505, 125, 360, 133, 143, 101, 15, 284, 540, 252, 14, 205, 140, 344, 26, 811, 138, 115, 48, 73, 34, 205, 316, 607, 63, 220, 7, 52, 150, 44, 52, 16, 40, 37, 158, 807, 37, 121, 12, 95, 10, 15, 35, 12, 131, 62, 115, 102, 807, 49, 53, 135, 138, 30, 31, 62, 67, 41, 85, 63, 10, 106, 807, 138, 8, 113, 20, 32, 33, 37, 353, 287, 140, 47, 85, 50, 37, 49, 47, 64, 6, 7, 71, 33, 4, 43, 47, 63, 1, 27, 600, 208, 230, 15, 191, 246, 85, 94, 511, 2, 270, 20, 39, 7, 33, 44, 22, 40, 7, 10, 3, 811, 106, 44, 486, 230, 353, 211, 200, 31, 10, 38, 140, 297, 61, 603, 320, 302, 666, 287, 2, 44, 33, 32, 511, 548, 10, 6, 250, 557, 246, 53, 37, 52, 83, 47, 320, 38, 33, 807, 7, 44, 30, 31, 250, 10, 15, 35, 106, 160, 113, 31, 102, 406, 230, 540, 320, 29, 66, 33, 101, 807, 138, 301, 316, 353, 320, 220, 37, 52, 28, 540, 320, 33, 8, 48, 107, 50, 811, 7, 2, 113, 73, 16, 125, 11, 110, 67, 102, 807, 33, 59, 81, 158, 38, 43, 581, 138, 19, 85, 400, 38, 43, 77, 14, 27, 8, 47, 138, 63, 140, 44, 35, 22, 177, 106, 250, 314, 217, 2, 10, 7, 1005, 4, 20, 25, 44, 48, 7, 26, 46, 110, 230, 807, 191, 34, 112, 147, 44, 110, 121, 125, 96, 41, 51, 50, 140, 56, 47, 152, 540, 63, 807, 28, 42, 250, 138, 582, 98, 643, 32, 107, 140, 112, 26, 85, 138, 540, 53, 20, 125, 371, 38, 36, 10, 52, 118, 136, 102, 420, 150, 112, 71, 14, 20, 7, 24, 18, 12, 807, 37, 67, 110, 62, 33, 21, 95, 220, 511, 102, 811, 30, 83, 84, 305, 620, 15, 2, 10, 8, 220, 106, 353, 105, 106, 60, 275, 72, 8, 50, 205, 185, 112, 125, 540, 65, 106, 807, 138, 96, 110, 16, 73, 33, 807, 150, 409, 400, 50, 154, 285, 96, 106, 316, 270, 205, 101, 811, 400, 8, 44, 37, 52, 40, 241, 34, 205, 38, 16, 46, 47, 85, 24, 44, 15, 64, 73, 138, 807, 85, 78, 110, 33, 420, 505, 53, 37, 38, 22, 31, 10, 110, 106, 101, 140, 15, 38, 3, 5, 44, 7, 98, 287, 135, 150, 96, 33, 84, 125, 807, 191, 96, 511, 118, 40, 370, 643, 466, 106, 41, 107, 603, 220, 275, 30, 150, 105, 49, 53, 287, 250, 208, 134, 7, 53, 12, 47, 85, 63, 138, 110, 21, 112, 140, 485, 486, 505, 14, 73, 84, 575, 1005, 150, 200, 16, 42, 5, 4, 25, 42, 8, 16, 811, 125, 160, 32, 205, 603, 807, 81, 96, 405, 41, 600, 136, 14, 20, 28, 26, 353, 302, 246, 8, 131, 160, 140, 84, 440, 42, 16, 811, 40, 67, 101, 102, 194, 138, 205, 51, 63, 241, 540, 122, 8, 10, 63, 140, 47, 48, 140, 288
The third paper is as follows:
317, 8, 92, 73, 112, 89, 67, 318, 28, 96,107, 41, 631, 78, 146, 397, 118, 98, 114, 246, 348, 116, 74, 88, 12, 65, 32, 14, 81, 19, 76, 121, 216, 85, 33, 66, 15, 108, 68, 77, 43, 24, 122, 96, 117, 36, 211, 301, 15, 44, 11, 46, 89, 18, 136, 68, 317, 28, 90, 82, 304, 71, 43, 221, 198, 176, 310, 319, 81, 99, 264, 380, 56, 37, 319, 2, 44, 53, 28, 44, 75, 98, 102, 37, 85, 107, 117, 64, 88, 136, 48, 151, 99, 175, 89, 315, 326, 78, 96, 214, 218, 311, 43, 89, 51, 90, 75, 128, 96, 33, 28, 103, 84, 65, 26, 41, 246, 84, 270, 98, 116, 32, 59, 74, 66, 69, 240, 15, 8, 121, 20, 77, 89, 31, 11, 106, 81, 191, 224, 328, 18, 75, 52, 82, 117, 201, 39, 23, 217, 27, 21, 84, 35, 54, 109, 128, 49, 77, 88, 1, 81, 217, 64, 55, 83, 116, 251, 269, 311, 96, 54, 32, 120, 18, 132, 102, 219, 211, 84, 150, 219, 275, 312, 64, 10, 106, 87, 75, 47, 21, 29, 37, 81, 44, 18, 126, 115, 132, 160, 181, 203, 76, 81, 299, 314, 337, 351, 96, 11, 28, 97, 318, 238, 106, 24, 93, 3, 19, 17, 26, 60, 73, 88, 14, 126, 138, 234, 286, 297, 321, 365, 264, 19, 22, 84, 56, 107, 98, 123, 111, 214, 136, 7, 33, 45, 40, 13, 28, 46, 42, 107, 196, 227, 344, 198, 203, 247, 116, 19, 8, 212, 230, 31, 6, 328, 65, 48, 52, 59, 41, 122, 33, 117, 11, 18, 25, 71, 36, 45, 83, 76, 89, 92, 31, 65, 70, 83, 96, 27, 33, 44, 50, 61, 24, 112, 136, 149, 176, 180, 194, 143, 171, 205, 296, 87, 12, 44, 51, 89, 98, 34, 41, 208, 173, 66, 9, 35, 16, 95, 8, 113, 175, 90, 56, 203, 19, 177, 183, 206, 157, 200, 218, 260, 291, 305, 618, 951, 320, 18, 124, 78, 65, 19, 32, 124, 48, 53, 57, 84, 96, 207, 244, 66, 82, 119, 71, 11, 86, 77, 213, 54, 82, 316, 245, 303, 86, 97, 106, 212, 18, 37, 15, 81, 89, 16, 7, 81, 39, 96, 14, 43, 216, 118, 29, 55, 109, 136, 172, 213, 64, 8, 227, 304, 611, 221, 364, 819, 375, 128, 296, 1, 18, 53, 76, 10, 15, 23, 19, 71, 84, 120, 134, 66, 73, 89, 96, 230, 48, 77, 26, 101, 127, 936, 218, 439, 178, 171, 61, 226, 313, 215, 102, 18, 167, 262, 114, 218, 66, 59, 48, 27, 19, 13, 82, 48, 162, 119, 34, 127, 139, 34, 128, 129, 74, 63, 120, 11, 54, 61, 73, 92, 180, 66, 75, 101, 124, 265, 89, 96, 126, 274, 896, 917, 434, 461, 235, 890, 312, 413, 328, 381, 96, 105, 217, 66, 118, 22, 77, 64, 42, 12, 7, 55, 24, 83, 67, 97, 109, 121, 135, 181, 203, 219, 228, 256, 21, 34, 77, 319, 374, 382, 675, 684, 717, 864, 203, 4, 18, 92, 16, 63, 82, 22, 46, 55, 69, 74, 112, 134, 186, 175, 119, 213, 416, 312, 343, 264, 119, 186, 218, 343, 417, 845, 951, 124, 209, 49, 617, 856, 924, 936, 72, 19, 28, 11, 35, 42, 40, 66, 85, 94, 112, 65, 82, 115, 119, 236, 244, 186, 172, 112, 85, 6, 56, 38, 44, 85, 72, 32, 47, 63, 96, 124, 217, 314, 319, 221, 644, 817, 821, 934, 922, 416, 975, 10, 22, 18, 46, 137, 181, 101, 39, 86, 103, 116, 138, 164, 212, 218, 296, 815, 380, 412, 460, 495, 675, 820, 952
The second cipher was successfully decrypted around 1885. Here, I will discuss the main considerations about this kind of cipher.
Since the numbers in the cipher far exceed the number of letters in the alphabet, we can assume that it is not a substitution nor a transposition cipher. So, we can assume that each number represents a letter, but this letter is obtained from a word contained in an external text. A cipher following this criterion is called a book cipher: in the case of a book cipher, a book or any other text could be used as a key. Now, the effective key here is the method of obtaining the letters from the text.
Using this system, the second cipher was decrypted by drawing on the United States Declaration of Independence. Assigning a number to each word of the referring text (the United States Declaration of Independence) and picking up the first letter of each word selected in the key (the list of the numbers, in this case, referred to the second cipher), we can extrapolate the plaintext. The extremely intelligent trick of this cipher is that the key text (the United States Declaration of Independence) is public but at the same time it was unknown to the entire world except for whom the message was intended. Only when someone holds the key (the list of the numbers) and the "key text" can they easily decrypt the message.
Let's look at the process of decrypting the second cipher:
- Assign to each word of the text a number in order from the first to the last word.
- Extrapolate the first letter of each word using the numbers contained in the cipher.
- Read the plaintext.
The following is the first part of the United States Declaration of Independence (until the 115th word) showing each word with its corresponding number:
When(1) in(2) the(3) course(4) of(5) human(6) events(7) it(8) becomes(9) necessary(10) for(11) one(12) people(13) to(14) dissolve(15) the(16) political(17) bands(18) which(19) have(20) connected(21) them(22) with(23) another(24) and(25) to(26) assume(27) among(28) the(29) powers(30) of(31) the(32) earth(33) the(34) separate(35) and(36) equal(37) station(38) to(39) which(40) the(41) laws(42) of(43) nature(44) and(45) of(46) nature's(47) god(48) entitle(49) them(50) a(51) decent(52) respect(53) to(54) the(55) opinions(56) of(57) mankind(58) requires(59) that(60) they(61) should(62) declare(63) the(64) causes(65) which(66) impel(67) them(68) to(69) the(70) separation(71) we(72) hold(73) these(74) truths(75) to(76) be(77) self(78) evident(79) that(80) all(81) men(82) are(83) created(84) equal(85) that(86) they(87) are(88) endowed(89) by(90) their(91) creator(92) with(93) certain(94) unalienable(95) rights(96) that(97) among(98) these(99) are(100) life(101) liberty(102) and(103) the(104) pursuit(105) of(106) happiness(107) that(108) to(109) secure(110) these(111) rights(112) governments(113) are(114) instituted(115) ...
The following numbers represent the first rows of the second cipher; as you can see, the bold words (with their corresponding numbers) correspond to the numbers we find in the ciphertext:
115, 73, 24, 807, 37, 52, 49, 17, 31, 62, 647, 22, 7, 15, 140, 47, 29, 107, 79, 84, 56, 239, 10, 26, 811, 5, 196, 308, 85, 52, 160, 136, 59, 211, 36, 9, 46, 316, 554, 122, 106, 95, 53, 58, 2, 42, 7, 35...
The following is the result of decryption using the cipher combined with the key text (the United States Declaration of Independence), picking up the first letter of each corresponding word, that is, the plaintext:
115 = instituted = I 73 = hold = h 24 = another = a 807 (missing) = v 37 = equal = e 52 = decent = d 49 = entitle = e
And so on…
I haven't included the entire United States Declaration of Independence; these are only the first 115 words. But if you want, you can visit http://www.unmuseum.org/bealepap.htm and try the exercise to rebuild the entire plaintext.
Here (with some missing letters) is the reconstruction of the first sentence:
I have deposited in the county of Bedford…….
If we carry on and compare the numbers with the corresponding numbers of the initial letters of the United States Declaration of Independence, the decryption will be as follows:
I have deposited in the county of Bedford, about four miles from Buford's, in an excavation or vault, six feet below the surface of the ground, the following articles, belonging jointly to the parties whose names are given in number "3," herewith:
The first deposit consisted of one thousand and fourteen pounds of gold, and three thousand eight hundred and twelve pounds of silver, deposited November, 1819. The second was made December, 1821, and consisted of nineteen hundred and seven pounds of gold, and twelve hundred and eighty-eight pounds of silver; also jewels, obtained in St. Louis in exchange for silver to save transportation, and valued at $13,000.
The above is securely packed in iron pots, with iron covers. The vault is roughly lined with stone, and the vessels rest on solid stone, and are covered with others. Paper number "1" describes the exact locality of the vault so that no difficulty will be had in finding it.
Many other cryptographers and cryptologists have tried to decrypt the first and third Beale ciphers in vain. Others, such as the treasure hunter Mel Fisher, who discovered hundreds of millions of dollars' worth of valuables under the sea, went to Bedford to search the area in order to find the treasure, without success.
Maybe Beale's tale is just a legend. Or maybe it is true, but nobody will ever know where the treasure is because nobody will decrypt the first cipher. Or, the treasure will never be unearthed because someone has already found it.
Anyway, what is really interesting in this story is the implementation of such a strong cipher without the help of any computers or electronic machines; it was just made with brainpower, a pen, and a sheet of paper.
Paradoxically, the number of attempts required to crack the cipher go from 1 to infinity assuming that the attacker works with brute force, exploring all the texts written in the world at that moment. On top of that, what happens if a key text is not public but was written by the transmitter himself and has been kept secret? In this case, if the cryptologist doesn't have the key (so doesn't hold the key text), the likelihood of them decrypting the cipher is zero.
The Beale cipher is also interesting because this kind of algorithm could have new applications in modern cryptography or in the future. Some of these applications could be related to methods of research for encrypted data in cloud computing.
The Vernam cipher
The Vernam cipher has the highest degree of security for a cipher, as it is theoretically completely secure. Since it uses a truly random key of the same length as the plaintext, it is called the perfect cipher. It's just a matter of entropy and randomness based on Shannon's principle of information entropy that determines an equal probability of each bit contained in the ciphertext. We will revisit this algorithm in Chapter 8, Quantum Cryptography, where we talk about quantum key distribution and the related method to encrypt the plaintext after determining the quantum key. Another interesting implementation is Hyper Crypto Satellite, which uses this algorithm to encrypt the plaintext crafted by a random key transmitted by a satellite radiocommunication and expressed as an infinite string of bits.
But for now, let's go on to explore the main characteristics of this algorithm.
The essential element of the algorithm is using the key only once per session. This feature makes the algorithm invulnerable to attacks against the ciphertext and even in the unlikely event that the key is stolen, it would be changed at the time of the next transmission.
The method is very simple: by adding the key to the message (mod 2) bit by bit, we will obtain the ciphertext. We will see this method, called XOR, many times throughout this book, especially when we discuss symmetric encryption in Chapter 2, Introduction to Symmetric Encryption. Just remember that the key has to be of the same length as the message.
A numerical example is as follows:
00101001(plaintext)10101100(key): Adding each bit (mod2)10000101(ciphertext)
Step 1: Transform the plaintext into a string of bits using ASCII code.
Step 2: Generate a random key of the same length as the plaintext.
Step 3: Encrypt by adding modulo 2 (XOR) of the plaintext bitwise to the key and obtain the ciphertext.
Step 4: Decrypt by making the inverse operation of adding the ciphertext to the key and obtain the plaintext again.
To make an example with numbers and letters, we will go back to HELLO. Let's assume that each letter corresponds to a number, starting from 0 = A, 1 = B, 2 = C, 3 = D, 4 = E … and so on until 25 = Z.
The random key is [DGHBC].
The encryption will present the following transposition:

Figure 1.10 – Encryption scheme in the Vernam algorithm
So, after transposing the letters, the encryption of [HELLO] is [KKSMQ].
You can create an exercise by yourself to decrypt the [KKSMQ] ciphertext using the inverse process: applying f(-K) to the ciphertext, returning the HELLO plaintext.
I would just like to remark that this algorithm is very strong if well implemented, following all the warnings and instructions to avoid a drastic reduction of security. One of the attacks that many algorithms suffer is well known as a ciphertext-only attack. This is successful if the attacker can deduce the plaintext, or even better the key, using the ciphertext or pieces of it. The most common techniques are frequency analysis and traffic analysis.
This algorithm is not vulnerable to ciphertext-only attacks. Moreover, if a piece of a key is known, it will be possible to decipher only the piece corresponding to the related bits. The rest of the ciphertext will be difficult to decrypt if it is long enough. However, the conditions regarding the implementation of this algorithm are very restrictive in order to obtain absolute invulnerability. First of all, the generation of the key has to be completely random. Second, the key and the message have to be of the same length, and third, there is always the problem of the key transmission.
This last problem affects all symmetric algorithms and is basically the problem that pushed cryptographers to invent asymmetric encryption to exchange keys between Alice and Bob (which we will see in the next chapter).
The second problem concerns the length of the key: if the message is too short, for instance, the word ten, to indicate the time of a military attack, the attacker could also rely on their good sense or on luck. It doesn't matter if there is a random key for a short message. The message could be decrypted intuitively if the attacker knows the topic of the transmission. On the other hand, if the message is very long, we are forced to use a very long key. In this case, the key will be very expensive to produce and expensive to transmit. Moreover, considering that for every new transmission the key has to be changed, the cost of implementing this cipher for commercial purposes is very high.
This is why, in general, mono-use strings such as this were used for military purposes during the Second World War and after. As I said before, this was the legendary algorithm used for the red line between Washington and Moscow to encrypt communications between the leaders of the US and the USSR during the Cold War.
Finally, we will analyze the implementation of this algorithm. It could be difficult to find a way to generate and transmit a random key, even if the security of the method is very high. In the last section of this book, I will show a new method for the transmission and the implementation of keys using the Vernam cipher combined with other algorithms and methods. This new one-time pad (OTP) system, named Hyper Crypto Satellite, could be used for both the authentication and the encryption of messages. I will also show you the possible vulnerabilities of the system and how to generate a very random key. The method was a candidate at the Satellite International Conference on Space, but at the time I decided not to present it to the public.

























































